练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．已知集合A={x|y=log2（x+1）}，集合B={x|{y=$\sqrt{1-x^2}}$}，则A∩B=（　　）
    A．（1，+∞）B．（-1，1]C．（0，+∞）D．（0，1）

    分析 根据集合的基本运算进行求解即可．

    解答 解：A={x|y=log2（x+1）}={x|x+1＞0}={x|x＞-1}，
    集合B={x|{y=$\sqrt{1-x^2}}$}={x|1-x2≥0}={x|-1≤x≤1}，
    则A∩B={x|-1＜x≤1}，
    故选：B．

    点评 本题主要考查集合的基本运算，求出集合的等价条件是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    3．如图，在直角坐标系中，曲线段AB是函数y=1-x2图象的一部分，P为曲线段AB上异于点A，B一个动点，PM丄x轴，垂足为M，PN丄y轴，垂足为N．
    （1）求PM+PN长度的范围；
    （2）求矩形PMON面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．某军区新兵50m步枪射击个人平均成绩x（单位：环）服从正态分布N（μ，o2），从这些个人平均成绩中随机抽取100个，得到如下频数分布表：
    x456789
    频数122640292
    （Ⅰ）求μ和o2的值（用样本数学期望、方差代替总体数学期望、方差）；
    （Ⅱ）如果这个军区有新兵10000名，试估计这个军区新兵50m步枪射击个人平均成绩在区间（7.9，8.8]上的人数[参考数据：$\sqrt{0.8}$=0.9，若ξ：N（μ，o2），则P（μ-o-＜ξ≤μ+o-）=0.6826，P（μ-2o-＜ξ≤μ+2o-）=0.9544，P（μ-3o-＜ξ≤μ+3o-=0.9974]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．1854年，地质学家W．K．劳夫特斯在森凯莱（古巴比伦地名）挖掘出两块泥板，其中一块泥板记着：
    92=81=60+21=1•21
    102=100=60+40=1•40
    112=121=2×60+1=2•1
    122=144=2×60+24=2•24
    …
    照此规律，582=56•4．（写成“a•b”的形式）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

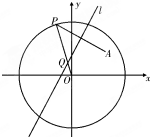    6．如图，已知点A为圆x2+y2=16内一定点，P是圆上任意一点，线段AP的垂直平分线l和半径OP相交于点Q，当点P在圆上运动时，点Q的轨迹是（　　）
    A．圆B．椭圆C．抛物线D．双曲线

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16． 已知函数$f（x）=2sin（2x+\frac{π}{6}）+1+a$，x∈[0，π]的最大值为2
    （1）在坐标系上做出函数y=f（x）的图象；
    （2）写出使f（x）+1≥0成立的x的取值集合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知集合A={-1，0，1，2}，集合B={x∈R|x2=1}，则A∩B=（　　）
    A．{1}B．{-1，1}C．{-1，0，1}D．{-1，0，1，2}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．现有甲、乙、丙三个儿童玩石头、剪刀、布的猜拳游戏，观察其出拳情况．
    （1）写出该试验的所有基本事件；
    （2）事件“三人不分胜负”发生的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知函数y=x3-bx2在[1，+∞）上是增函数，则实数b的取值范围是（-∞，$\frac{3}{2}$]．

    查看答案和解析>>

    同步练习册答案