
【题目】在正三角形![]() 中,
中,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 边上的点,满足
边上的点,满足![]()
![]() (如图1).将△
(如图1).将△![]() 沿
沿![]() 折起到
折起到![]() 的位置,使二面角
的位置,使二面角![]() 成直二面角,连结
成直二面角,连结![]() 、
、![]() (如图2)
(如图2)


(Ⅰ)求证:![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)取BE的中点D,连结DF∵AE![]() EB=CF
EB=CF![]() FA=1
FA=1![]() 2,∴AF=AD=2,而∠A=600,∴△ADF是正三角形,AE=DE=1,∴EF⊥AD,在图2中,A1E⊥EF,BE⊥EF,∴∠A1EB为二面角A1-EF-B的平面角.∴A1E⊥BE∴A1E⊥平面BEF,即A1E⊥平面BEP(Ⅱ)
2,∴AF=AD=2,而∠A=600,∴△ADF是正三角形,AE=DE=1,∴EF⊥AD,在图2中,A1E⊥EF,BE⊥EF,∴∠A1EB为二面角A1-EF-B的平面角.∴A1E⊥BE∴A1E⊥平面BEF,即A1E⊥平面BEP(Ⅱ)![]()
【解析】
试题不妨设正三角形ABC 的边长为 3 .

(I)在图1中,取BE的中点D,连结DF.
∵AE![]() EB=CF
EB=CF![]() FA=1
FA=1![]() 2,∴AF=AD=2,而∠A=600,∴△ADF是正三角形,
2,∴AF=AD=2,而∠A=600,∴△ADF是正三角形,
又AE=DE=1,∴EF⊥AD. 2分
在图2中,A1E⊥EF,BE⊥EF,∴∠A1EB为二面角A1-EF-B的平面角.
由题设条件知此二面角为直二面角,∴A1E⊥BE.
又BE∩EF=E,∴A1E⊥平面BEF,即A1E⊥平面BEP. .4分
(II)建立分别以ED、EF、EA为x轴、y轴、z轴的空间直角坐标系,则E(0,0,0),A(0,0,1),
B(2,0,0),F(0, ![]() ,0), P (1,
,0), P (1, ![]() ,0),则,
,0),则,![]() .
.
设平面ABP的法向量为![]() ,
,
由![]() 平面ABP知,
平面ABP知,![]() ,即
,即
 令
令![]() ,得
,得![]() ,
,![]() .
.
![]() ,设平面AFP的法向量为
,设平面AFP的法向量为![]() .
.
由![]() 平面AFP知,
平面AFP知,![]() ,即
,即
 令
令![]() ,得
,得![]() ,
,![]() .
.
 ,
,
所以二面角B-A1P-F的余弦值是![]() 13分
13分


科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥D-ABC中,二面角A-BC-D的大小为90°,且∠BDC=90°,∠ABC=30°,BC=3,![]() .
.
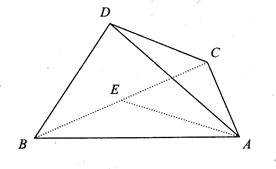
(1)求证:AC⊥平面BCD;
(2)二面角B-AC-D为45°,且E为线段BC的中点,求直线AE与平面ACD所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆![]() :
: ![]() ,长轴的右端点与抛物线
,长轴的右端点与抛物线![]() :
: ![]() 的焦点
的焦点![]() 重合,且椭圆
重合,且椭圆![]() 的离心率是
的离心率是![]() .
.
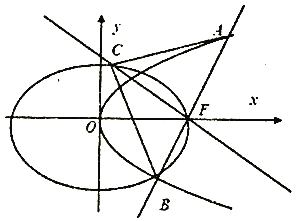
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 作直线
作直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
, ![]() 两点,过
两点,过![]() 且与直线
且与直线![]() 垂直的直线交椭圆
垂直的直线交椭圆![]() 于另一点
于另一点![]() ,求
,求![]() 面积的最小值,以及取到最小值时直线
面积的最小值,以及取到最小值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,且经过点
,且经过点![]() .
.
![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]() 过点
过点![]() 且不与
且不与![]() 轴重合的直线
轴重合的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() 分别交椭圆
分别交椭圆![]() 于点
于点![]() ,设
,设![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图像向左平移
的图像向左平移![]() 个单位后得到函数
个单位后得到函数![]() 的图像,且函数
的图像,且函数![]() 满足
满足![]() ,则下列命题中正确的是()
,则下列命题中正确的是()
A. 函数![]() 图像的两条相邻对称轴之间的距离为
图像的两条相邻对称轴之间的距离为![]()
B. 函数![]() 图像关于点
图像关于点![]() 对称
对称
C. 函数![]() 图像关于直线
图像关于直线![]() 对称
对称
D. 函数![]() 在区间
在区间![]() 内为单调递减函数
内为单调递减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
该社团将该校区在2018年11月中10天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
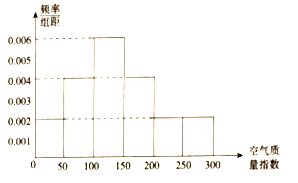
(1)以这10天的空气质量指数监测数据作为估计2018年11月的空气质量情况,则2018年11月中有多少天的空气质量达到优良?
(2)从这10天的空气质量指数监测数据中,随机抽取三天,求恰好有一天空气质量良的概率;
(3)从这10天的数据中任取三天数据,记![]() 表示抽取空气质量良的天数,求
表示抽取空气质量良的天数,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极坐标建立极坐标系,圆
轴正半轴为极坐标建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
![]() 求
求![]() 的普通方程;
的普通方程;
![]() 将圆
将圆![]() 平移,使其圆心为
平移,使其圆心为![]() ,设
,设![]() 是圆
是圆![]() 上的动点,点
上的动点,点![]() 与
与![]() 关于原点
关于原点![]() 对称,线段
对称,线段![]() 的垂直平分线与
的垂直平分线与![]() 相交于点
相交于点![]() ,求
,求![]() 的轨迹的参数方程.
的轨迹的参数方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com