
【题目】如图,在四棱锥 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是 ![]() 的中点,
的中点, ![]() 是棱
是棱 ![]() 上的点,
上的点, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)求证:平面 ![]() 底面
底面 ![]() ;
;
(2)设 ![]() ,若二面角
,若二面角 ![]() 的平面角的大小为
的平面角的大小为 ![]() ,试确定
,试确定 ![]() 的值.
的值.
【答案】
(1)
证明:∵AD//BC,BC= ![]() ,Q是AD的中点,
,Q是AD的中点,
∴BC ![]() DQ,则四边形BCDQ为平行四边形,从而CD//BQ.
DQ,则四边形BCDQ为平行四边形,从而CD//BQ.
∵AD⊥CD,∴QB⊥AD.
∵PA=PD=2,AD=2,Q是AD的中点,∴ ![]()
又∵QB=CD= ![]() ,
, ![]()
∴ ![]() ,即PQ⊥QB,又PQ
,即PQ⊥QB,又PQ ![]() AD=Q,∴BQ⊥平面PAD,∴平面PAD⊥底面ABCD.
AD=Q,∴BQ⊥平面PAD,∴平面PAD⊥底面ABCD.
(2)
解:∵PA=PD=2,Q是AD的中点,∴PQ⊥AD.∵平面PAD⊥平面ABCD,且平面PAD ![]() 平面ABCD=AD,∴PQ⊥平面ABCD.如图,以Q为原点建空间直角坐标系.
平面ABCD=AD,∴PQ⊥平面ABCD.如图,以Q为原点建空间直角坐标系.
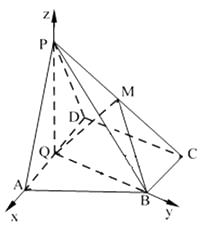
则平面BQC的法向量为 ![]()
设 ![]() ,则
,则 ![]() ,∵
,∵ ![]() ,∴
,∴ ![]()
则 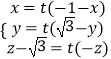 ,即
,即 ![]() ,
, ![]() ,
, ![]() ,在平面MBQ中,
,在平面MBQ中, ![]() ,
, ![]() ,设平面MBQ的法向量为
,设平面MBQ的法向量为 ![]() ,由
,由 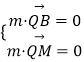 ,得
,得 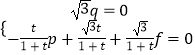 ,取f=t,得
,取f=t,得 ![]() .∴平面MBQ的一个法向量为
.∴平面MBQ的一个法向量为 ![]()
∵二面角M-BQ-C的平面角的大小为30°,∴ 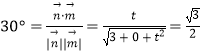 ,解得t=3.
,解得t=3.
【解析】本题主要考查空间直线与平面垂直、平面与平面垂直、直线与直线垂直的判定与性质,二面角等基础知识,考查空间想象能力,推理论证能力,运算求解能力,以及数形结合思想、化归与转化思想.
【考点精析】通过灵活运用直线与平面垂直的判定和平面与平面垂直的判定,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;一个平面过另一个平面的垂线,则这两个平面垂直即可以解答此题.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】设a为实数,给出命题p:函数f(x)=(a﹣ ![]() )x是R上的减函数,命题q:关于x的不等式(
)x是R上的减函数,命题q:关于x的不等式( ![]() )|x﹣1|≥a的解集为.
)|x﹣1|≥a的解集为.
(1)若p为真命题,求a的取值范围;
(2)若q为真命题,求a的取值范围;
(3)若“p且q”为假命题,“p或q”为真命题,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度![]() (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度![]() (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当![]() 不超过
不超过![]() 尾/立方米时,
尾/立方米时, ![]() 的值为
的值为![]() 千克/年;当
千克/年;当![]() 时,
时, ![]() 是
是![]() 的一次函数,且当
的一次函数,且当![]() 时,
时, ![]() .
.
(![]() )当
)当![]() 时,求
时,求![]() 关于
关于![]() 的函数的表达式.
的函数的表达式.
(![]() )当养殖密度
)当养殖密度![]() 为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点列An(an , bn)(n∈N*)均为函数y=ax(a>0,a≠1)的图象上,点列Bn(n,0)满足|AnBn|=|AnBn+1|,若数列{bn}中任意连续三项能构成三角形的三边,则a的取值范围为( )
A.(0, ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
B.( ![]() ,1)∪(1,
,1)∪(1, ![]() )
)
C.(0, ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
D.( ![]() ,1)∪(1,
,1)∪(1, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U={1,2,3,4,5,6,7},集合A={1,3,7},B={x|x=log2(a+1),a∈A},则A∩B=( )
A.{1,3}
B.{5,6}
C.{4,5,6}
D.{4,5,6,7}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率
的离心率 ![]() ,过点A(0,﹣b)和B(a,0)的直线与原点的距离为
,过点A(0,﹣b)和B(a,0)的直线与原点的距离为 ![]() .
.
(1)求椭圆的方程;
(2)已知定点E(﹣1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点,问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com