
【题目】已知数列![]() 的各项均为整数,其前n项和为
的各项均为整数,其前n项和为![]() .规定:若数列
.规定:若数列![]() 满足前r项依次成公差为1的等差数列,从第
满足前r项依次成公差为1的等差数列,从第![]() 项起往后依次成公比为2的等比数列,则称数列
项起往后依次成公比为2的等比数列,则称数列![]() 为“r关联数列”.
为“r关联数列”.
(1)若数列![]() 为“6关联数列”,求数列
为“6关联数列”,求数列![]() 的通项公式;
的通项公式;
(2)在(1)的条件下,求出![]() ,并证明:对任意
,并证明:对任意![]() ,
,![]() ;
;
(3)若数列![]() 为“6关联数列”,当
为“6关联数列”,当![]() 时,在
时,在![]() 与
与![]() 之间插入n个数,使这
之间插入n个数,使这![]() 个数组成一个公差为
个数组成一个公差为![]() 的等差数列,求
的等差数列,求![]() ,并探究在数列
,并探究在数列![]() 中是否存在三项
中是否存在三项![]() ,
,![]() ,
,![]() 其中m,k,p成等差数列)成等比数列?若存在,求出这样的三项;若不存在,说明理由.
其中m,k,p成等差数列)成等比数列?若存在,求出这样的三项;若不存在,说明理由.
【答案】(1)![]()
(2)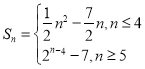 ,证明见解析
,证明见解析
(3)![]() ,不存在,理由见解析
,不存在,理由见解析
【解析】
(1)根据题意得到![]() ,
,![]() ,且
,且![]() .解得
.解得![]() 即可求出
即可求出![]() 的通项公式.
的通项公式.
(2)由(1)得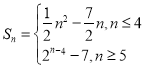 ,利用换元法证明数列
,利用换元法证明数列![]() 的最小项为
的最小项为![]() ,即可证明对任意
,即可证明对任意![]() ,
,![]() .
.
(3)由(1)可知,当![]() 时,
时,![]() ,由此可得出
,由此可得出![]() .假设在数列
.假设在数列![]() 中存在三项
中存在三项![]() ,
,![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() 成等差数列)成等比数列,则
成等差数列)成等比数列,则![]() ,推导出故
,推导出故![]() ,这与题设矛盾,所以在数列
,这与题设矛盾,所以在数列![]() 中不存在三项
中不存在三项![]() ,
,![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() 成等差数列)成等比数列.
成等差数列)成等比数列.
(1)∵![]() 为“6关联数列”,
为“6关联数列”,
∴![]() 前6项为等差数列,从第5项起为等比数列.
前6项为等差数列,从第5项起为等比数列.
∴![]() ,
,![]() ,且
,且![]() .
.
即![]() ,解得
,解得![]() .
.
∴![]() .
.
(2)由(1)得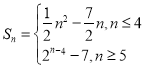 .
.
![]() :
:![]() ,
,
![]() :
:![]() ,
,
![]() :
:![]() ,
,
可见数列![]() 的最小项为
的最小项为![]() .
.
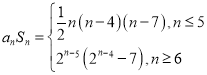 ,
,
由列举法知:当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() (
(![]() ),
),
设![]() ,则
,则![]() ,
,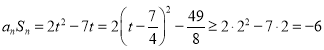 .
.
(3)由(1)可知,当![]() 时,
时,![]() ,
,
因为:![]() ,
,![]() .
.
故:![]() .
.
假设在数列![]() 中存在三项
中存在三项![]() ,
,![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() 成等差数列)成等比数列,
成等差数列)成等比数列,
则:![]() ,即:
,即: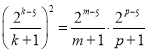 ,
,
即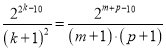 (*)
(*)
因为![]() ,
,![]() ,
,![]() 成等差数列,所以
成等差数列,所以![]() ,
,
(*)式可以化简为![]() ,
,
即:![]() ,故
,故![]() ,这与题设矛盾.
,这与题设矛盾.
所以在数列![]() 中不存在三项
中不存在三项![]() ,
,![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() 成等差数列)成等比数列.
成等差数列)成等比数列.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() 为其前
为其前![]() 项的和,满足
项的和,满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:当
,求证:当![]() ,
,![]() 时
时![]() ;
;
(3)已知当![]() ,且
,且![]() 时有
时有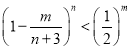 ,其中
,其中![]() ,求满足
,求满足![]() 的所有
的所有![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题:“若![]() ,
,![]() 为异面直线,平面
为异面直线,平面![]() 过直线
过直线![]() 且与直线
且与直线![]() 平行,则直线
平行,则直线![]() 与平面
与平面![]() 的距离等于异面直线
的距离等于异面直线![]() ,
,![]() 之间的距离”为真命题.根据上述命题,若
之间的距离”为真命题.根据上述命题,若![]() ,
,![]() 为异面直线,且它们之间的距离为
为异面直线,且它们之间的距离为![]() ,则空间中与
,则空间中与![]() ,
,![]() 均异面且距离也均为
均异面且距离也均为![]() 的直线
的直线![]() 的条数为( )
的条数为( )
A.0条B.1条C.多于1条,但为有限条D.无数多条
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于由有限个自然数组成的集合A,定义集合S(A)={a+b|a∈A,b∈A},记集合S(A)的元素个数为d(S(A)).定义变换T,变换T将集合A变换为集合T(A)=A∪S(A).
(1)若A={0,1,2},求S(A),T(A);
(2)若集合A有n个元素,证明:“d(S(A))=2n-1”的充要条件是“集合A中的所有元素能组成公差不为0的等差数列”;
(3)若A{1,2,3,4,5,6,7,8}且{1,2,3,…,25,26}T(T(A)),求元素个数最少的集合A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=xv(x)可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,且经过点
的中心在坐标原点,且经过点![]() ,它的一个焦点与抛物线E:
,它的一个焦点与抛物线E:![]() 的焦点重合,斜率为k的直线l交抛物线E于A、B两点,交椭圆
的焦点重合,斜率为k的直线l交抛物线E于A、B两点,交椭圆![]() 于C、D两点.
于C、D两点.
(1)求椭圆![]() 的方程;
的方程;
(2)直线l经过点![]() ,设点
,设点![]() ,且
,且![]() 的面积为
的面积为![]() ,求k的值;
,求k的值;
(3)若直线l过点![]() ,设直线
,设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差数列,求直线l的方程.
成等差数列,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了普及环保知识,增强学生的环保意识,在全校组织了一次有关环保知识的竞赛,经过初赛、复赛,甲、乙两个代表队(每队![]() 人)进入了决赛,规定每人回答一个问题,答对为本队赢得
人)进入了决赛,规定每人回答一个问题,答对为本队赢得![]() 分,答错得
分,答错得![]() 分,假设甲队中每人答对的概率均为
分,假设甲队中每人答对的概率均为![]() ,乙队中
,乙队中![]() 人答对的概率分別为
人答对的概率分別为![]() ,且各人回答正确与否相互之间没有影响,用
,且各人回答正确与否相互之间没有影响,用![]() 表示乙队的总得分.
表示乙队的总得分.
(1)求![]() 的分布列;
的分布列;
(2)求甲、乙两队总得分之和等于![]() 分且甲队获胜的概率.
分且甲队获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中,真命题是( )
A.和两条异面直线都相交的两条直线是异面直线
B.和两条异面直线都相交于不同点的两条直线是异面直线
C.和两条异面直线都垂直的直线是异面直线的公垂线
D.若![]() 、
、![]() 是异面直线,
是异面直线,![]() 、
、![]() 是异面直线,则
是异面直线,则![]() 、
、![]() 是异面直线
是异面直线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com