
 ,
, V2S,又d=
V2S,又d= S时,V=25
S时,V=25 ,
, 时,车距d=车身长的一半,车流量Q=
时,车距d=车身长的一半,车流量Q=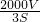 ,∴Qmax=
,∴Qmax=
 时,车距d=
时,车距d= V2S,车流量Q=
V2S,车流量Q=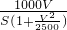 =
=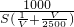 ≤
≤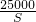
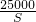 >
>


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:填空题
| 年份 | 2004 | 2006 | 2008 | 2010 |
| 需求量(万吨) | 255 | 264 | 276 | 285 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
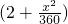 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
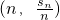 (n∈N+)均在函数y=3x-2的图象上.
(n∈N+)均在函数y=3x-2的图象上.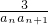 ,Tn是数列{bn}的前n项和,求使得Tn
,Tn是数列{bn}的前n项和,求使得Tn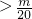 对所有n∈N+都成立的最大正整数m.
对所有n∈N+都成立的最大正整数m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com