练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知是抛物线的焦点，点在轴上，为坐标原点，且满足，经过点且垂直于轴的直线与抛物线交于、两点，且.

    （1）求抛物线的方程；

    （2）直线与抛物线交于、两点，若，求点到直线的最大距离.

    【答案】（1）；（2）.

    【解析】

    （1）求得点的坐标，可得出直线的方程，与抛物线的方程联立，结合求出正实数的值，进而可得出抛物线的方程；

    （2）设点，，设的方程为，将直线的方程与抛物线的方程联立，列出韦达定理，结合求得的值，可得出直线所过定点的坐标，由此可得出点到直线的最大距离.

    （1）易知点，又，所以点，则直线的方程为.

    联立，解得或，所以.

    故抛物线的方程为；

    （2）设的方程为，联立有，

    设点，，则，所以.

    所以，解得.

    所以直线的方程为，恒过点.

    又点，故当直线与轴垂直时，点到直线的最大距离为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，

    （1）求的最大值；

    （2）若对于任意的，不等式恒成立，求整数a的最小值.（参考数据，）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某汽车品牌为了解客户对其旗下的五种型号汽车的满意情况，随机抽取了一些客户进行回访，调查结果如下表：

    汽车型号

    Ⅰ

    Ⅱ

    Ⅲ

    Ⅳ

    Ⅴ

    回访客户（人数）

    250

    100

    200

    700

    350

    满意率

    0.5

    0.3

    0.6

    0.3

    0.2

    满意率是指某种型号汽车的回访客户中，满意人数与总人数的比值．假设客户是否满意互相独立，且每种型号汽车客户对于此型号汽车满意的概率与表格中该型号汽车的满意率相等．

    （1）从所有的回访客户中随机抽取1人，求这个客户满意的概率；

    （2）从Ⅰ型号和Ⅴ型号汽车的所有客户中各随机抽取1人，设其中满意的人数为，求的分布列和期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正方形，分别是的中点，将沿折起，如图所示，记二面角的大小为

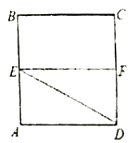
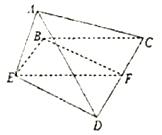
    （1）证明：

    （2）若为正三角形，试判断点在平面内的身影是否在直线上，证明你的结论，并求角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2017年冬，北京雾霾天数明显减少，据环保局统计三个月的空气质量，达到优良的天数超过天，重度污染的天数仅有天，主要原因是政府对治理雾霾采取有效措施．如：（1）减少机动车尾气排放（2）实施煤改电或煤改气工程（3）关停了大量的排污企业（4）部分企业季节性停产．为了解农村地区实施煤改气工程后天然气的使用从某乡镇随机抽取户，进行月均用气量调查，得到的用气量数据均在区间内，表如下

    分组

    频数

    频率

    14

    0.14

    55

    0.55

    4

    0.04

    2

    0.02

    合计

    100

    1

    （1）求和值，若同组内的每个数据用该组区间中点值代替，估计该乡镇每户平均用气量；

    （2）从样本调查的用气量和的用户组中任选2户，进行燃气使用满意度调查，求2户用气量处于不同区间的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

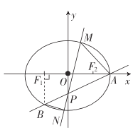
    【题目】如图，椭圆的右顶点为，左、右焦点分别为、，过点且斜率为的直线与轴交于点，与椭圆交于另一个点，且点在轴上的射影恰好为点．

    （1）求点的坐标；

    （2）过点且斜率大于的直线与椭圆交于两点，若，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面是等腰梯形，，，是等边三角形，点在上，且．

    （1）证明：//平面．

    （2）若平面平面，求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若在上单调递增，求实数的取值范围；

    （2）若时，求证：对于任意的，均有.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（2017高考新课标Ⅲ，理19）如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．

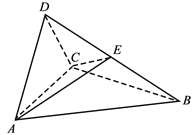
    （1）证明：平面ACD⊥平面ABC；

    （2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D–AE–C的余弦值.

    查看答案和解析>>

    同步练习册答案