
 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=$\sqrt{2}$,AF=1,M是线段EF的中点.
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=$\sqrt{2}$,AF=1,M是线段EF的中点.分析 (1)要证AM∥平面BDE,直线证明直线AM平行平面BDE内的直线OE即可;
(2)在平面AFD中过A作AS⊥DF于S,连接BS,说明∠BSA是二面角A-DF-B的平面角,然后求二面角A-DF-B的大小.
(3)设出线段AC上P点的坐标,由PF与CD所成的角是60°,得到向量夹角的余弦值为$\frac{1}{2}$,得到关于t 的等式,由此可求得P点的坐标
解答 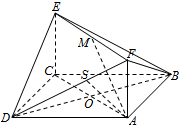 解:(1)记AC与BD的交点为O,连接OE,
解:(1)记AC与BD的交点为O,连接OE,
∵O、M分别是AC、EF的中点,ACEF是矩形,
∴四边形AOEM是平行四边形,
∴AM∥OE
∵OE?平面BDE,AM?平面BDE,
∴AM∥平面BDE
(2)在平面AFD中过A作AS⊥DF于S,连接BS,
∵AB⊥AF,AB⊥AD,AD∩AF=A,
∴AB⊥平面ADF,
∴AS是BS在平面ADF上的射影,
由三垂线定理得BS⊥DF
∴∠BSA是二面角A-DF-B的平面角
在Rt△ASB中,AS=$\frac{AD•AF}{DF}$=$\frac{\sqrt{6}}{3}$,AB=$\sqrt{2}$,
∴tan∠ASB=$\sqrt{3}$,∠ASB=60°,
∴二面角A-DF-B的大小为60°;
(3)如图 设P(t,t,0)(0≤t≤$\sqrt{2}$),
设P(t,t,0)(0≤t≤$\sqrt{2}$),
则$\overrightarrow{PF}$=($\sqrt{2}$-t,$\sqrt{2}$-t,1),$\overrightarrow{CD}$=($\sqrt{2}$,0,0)
又∵$\overrightarrow{PF}$,$\overrightarrow{CD}$夹角为60°,∴$\frac{|2-\sqrt{2}t|}{\sqrt{(\sqrt{2}-t)^{2}+(\sqrt{2}-t)^{2}+1}•\sqrt{2}}=\frac{1}{2}$,
解之得t=$\frac{\sqrt{2}}{2}$或t=$\frac{3\sqrt{2}}{2}$(舍去),
故点P为AC的中点时满足题意.
点评 本题考查直线与平面平行,二面角的知识,考查空间想象能力,逻辑思维能力,是中档题;(1,2也可以利用空间直角坐标系)


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 若求得相关系数r=-0.89,则y与x具备很强的线性相关关系,且为负相关 | |
| B. | 同学甲根据这组数据得到的回归模型1的残差平方和E1=1.8,同学乙根据这组数据得到的回归模型2的残差平方和E2=2.4,则模型1的拟合效果更好 | |
| C. | 用相关指数R2来刻画回归效果,模型1的相关指数R12=0.48,模型2的相关指数R22=0.91,则模型1的拟合效果更好 | |
| D. | 该回归分析只对被调查样本的总体适用 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | ab<b2 | C. | ac2<bc2 | D. | a2>ab>b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com