
【题目】已知圆 ![]() 的圆心在直线
的圆心在直线 ![]() 上,且圆
上,且圆 ![]() 经过点
经过点 ![]() .
.
(1)求圆的标准方程;
(2)直线 ![]() 过点
过点 ![]() 且与圆
且与圆 ![]() 相交,所得弦长为4,求直线
相交,所得弦长为4,求直线 ![]() 的方程.
的方程.
【答案】
(1)解:设圆心为 ![]() ,则
,则 ![]() 应在
应在 ![]() 的中垂线上,其方程为
的中垂线上,其方程为 ![]() ,
,
由 ![]() ,即圆心
,即圆心 ![]() 坐标为
坐标为 ![]()
又半径 ![]() ,故圆的方程为
,故圆的方程为 ![]()
(2)解:点 ![]() 在圆内,且弦长为
在圆内,且弦长为 ![]() ,故应有两条直线.
,故应有两条直线.
圆心到直线距离 ![]() .
.
①当直线的斜率不存在时,直线的方程为 ![]() ,
,
此时圆心到直线距离为1,符合题意.
②当直线的斜率存在时,设为 ![]() ,直线方程为
,直线方程为 ![]()
整理为 ![]() ,则圆心到直线距离为
,则圆心到直线距离为 ![]()
解得 ![]() ,直线方程为
,直线方程为 ![]()
综上①②,所求直线方程为 ![]() 或
或 ![]()
【解析】(1)圆心为 两条弦所在直线相交点,利用方程组求出圆心,两点距离求出半径,得到圆的标准方程 。
(2)讨论斜率存在与否 ,设出直线方程, 利用垂径定理求出圆心到直线的距离,由点到直线距离公式求出斜率K,得到直线方程。


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】某校为调查高一、高二学生周日在家学习用时情况,随机抽取了高一、高二各![]() 人,对他们的学习时间进行了统计,分别得到了高一学生学习时间(单位:小时)的频数分布表和高二学生学习时间的频率分布直方图.
人,对他们的学习时间进行了统计,分别得到了高一学生学习时间(单位:小时)的频数分布表和高二学生学习时间的频率分布直方图.
高一学生学习时间的频数分布表(学习时间均在区间![]() 内):
内):
学习时间 |
|
|
|
|
|
|
频数 | 3 | 1 | 8 | 4 | 2 | 2 |
高二学生学习时间的频率分布直方图:
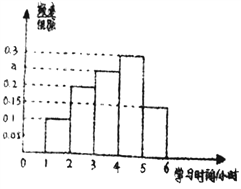
(1)求高二学生学习时间的频率分布直方图中的![]() 值,并根据此频率分布直方图估计该校高二学生学习时间的中位数;
值,并根据此频率分布直方图估计该校高二学生学习时间的中位数;
(2)利用分层抽样的方法,从高一学生学习时间在![]() ,
,![]() 的两组里随机抽取
的两组里随机抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人,求学习时间在
人,求学习时间在![]() 这一组中至少有
这一组中至少有![]() 人被抽中的概率.
人被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,点
,点![]() 在直线
在直线![]() 上.数列
上.数列![]() 满足
满足
![]()
![]() ,
,![]() ,且其前9项和为153.
,且其前9项和为153.
(Ⅰ)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求使不等式
,求使不等式![]() 对一切
对一切![]() 都成立的最大正整数
都成立的最大正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线 ![]() 的焦点为
的焦点为 ![]() ,其准线与
,其准线与 ![]() 轴交于点
轴交于点 ![]() ,过
,过 ![]() 作斜率为
作斜率为 ![]() 的直线
的直线 ![]() 与抛物线交于
与抛物线交于 ![]() 两点,弦
两点,弦 ![]() 的中点为
的中点为 ![]() 的垂直平分线与
的垂直平分线与 ![]() 轴交于
轴交于 ![]() .
.
(1)求 ![]() 的取值范围;
的取值范围;
(2)求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 中,
中, ![]() ,
, ![]() 分别是
分别是 ![]() 的中点,将
的中点,将 ![]() 沿
沿 ![]() 折起成
折起成 ![]() ,使面
,使面 ![]() 面
面 ![]() ,
, ![]() 分别是
分别是 ![]() 和
和 ![]() 的中点,平面
的中点,平面 ![]() 与
与 ![]() ,
, ![]() 分别交于点
分别交于点 ![]() .
.
(1)求证: ![]() ;
;
(2)求二面角 ![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王在年初用50万元购买一辆大货车,第一年因缴纳各种费用需支出6万元,从第二年起,每年都比上一年增加支出2万元,假定该车每年的运输收入均为25万元.小王在该车运输累计收入超过总支出后,考虑将大货车作为二手车出售,若该车在第x年年底出售,其销售价格为25-x万元(国家规定大货车的报废年限为10年).
(1)大货车运输到第几年年底,该车运输累计收入超过总支出?
(2)在第几年年底将大货车出售,能使小王获得的年平均利润最大(利润=累计收入+销售收入-总支出)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com