练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知P＝{|＝（－1,1）＋n（1,2），n∈R}，Q＝{|＝（1，－2）＋n（2,3），n∈R}是两个向量集合， 则P∩Q等于　　　　　　　　　　　　　　　　　　　　　　　 （ 　）

    　　　 A．{（1，－2）}　　　　　　　　　　　　　 B．{（－23，－13）} 　　　　　　　　　　　

    　　 C．φ　　　 　　　　 　　　　　　　　　　　　　　　 D．{（－13，－23）}

    D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：重庆武隆中学2005～2006年高二数学期末模拟考试题 题型：013

    已知P＝(3cosα，3sinα，1)和Q＝(2cosβ，2sinβ，1)，则|PQ|的取值范围是

    [　　]

    A．[1，5]

    B．(1，5)

    C．[0，5]

    D．[0，25]

    查看答案和解析>>

    科目：高中数学 来源：新疆兵团二中2012届高三第六次月考数学文科试题 题型：013

    已知P＝{－1，0，}，Q＝{y/y＝sin，∈R}，则P∩Q＝

    [　　]

    A．

    B．{0}

    C．{－1，0}

    D．9{－1，0，}

    查看答案和解析>>

    科目：高中数学 来源：江西九江市2011届高三第一次六校联考理科数学试题 题型：044

    已知关于x的二次函数f(x)＝ax2－4bx＋1

    (1)设集合P＝{－1，1，2，3，4，5}和Q＝{－2，－1，1，2，3，4}，分别从集合P和Q中随机取一个数作为a和b，求函数y＝f(x)在区间[1，＋∞]上是增函数的概率；

    (2)设点(a，b)是区域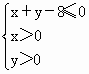内的随机点，求函数y＝f(x)在区间[1，＋∞)上是增函数的概率．

    查看答案和解析>>

    科目：高中数学 来源：山东省莱州一中2012届高三上学期模块检测数学文科试题 题型：044

    已知函数f(x)＝x3＋ax2＋bx＋c．，且曲线y＝f(x)上的点P(1，f(1))处的切线方程为y＝3x＋1．

    (1)若y＝f(x)在x＝－2时有极值，求f(x)的表达式；

    (2)若函数y＝f(x)在区间[－2，1]上单调递增，求b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2014届山东省高一第二学期期中考试数学试卷（解析版） 题型：解答题

    已知sina＝,aÎ(,p)，cosb＝－，b是第三象限的角.

    ⑴ 求cos(a－b)的值；

    ⑵ 求sin(a＋b)的值；

    ⑶ 求tan2a的值.

    【解析】第一问中∵ aÎ(,p),∴ cosa＝－＝－,  ∵ b是第三象限的角，

    ∴ sinb＝－＝－,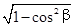     

    cos(a－b)＝cosa·cosb＋sina·sinb ＝(－)×(－)＋×(－)＝－ 

    ⑵ 中sin(a＋b)＝sina·cosb＋cosa·sinb       ＝×(－)＋(－)×(－)＝ ⑶ 利用二倍角的正切公式得到。∵tana＝＝－ ∴tan2a＝ ＝＝－ 

    解∵ aÎ(,p),∴ cosa＝－＝－,         …………1分

    ∵ b是第三象限的角，∴ sinb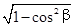＝－＝－,        ………2分

    ⑴ cos(a－b)＝cosa·cosb＋sina·sinb          …………3分

    ＝(－)×(－)＋×(－)＝－          ………………5分

    ⑵ sin(a＋b)＝sina·cosb＋cosa·sinb          ……………………6分

    ＝×(－)＋(－)×(－)＝           …………………8分

    ⑶ ∵tana＝＝－             …………………9分

    ∴tan2a＝             ………………10分

    ＝＝－

     

    查看答案和解析>>

    同步练习册答案