
【题目】某医院治疗白血病有甲、乙两套方案,现就70名患者治疗后复发的情况进行了统计,得到其等高条形图如图所示(其中采用甲、乙两种治疗方案的患者人数之比为![]() ).
).

(1)补充完整![]() 列联表中的数据,并判断是否有
列联表中的数据,并判断是否有![]() 的把握认为甲、乙两套治疗方案对患者白血病复发有影响;
的把握认为甲、乙两套治疗方案对患者白血病复发有影响;

(2)从复发的患者中抽取3人进行分析,求其中接受“乙方案”治疗的人数![]() 的数学期望.
的数学期望.
附:
|
|
|
|
|
|
|
|
|
|
 ,其中
,其中![]() .
.
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() ,动圆P与圆M相外切,且与直线l相切.设动圆圆心P的轨迹为E.
,动圆P与圆M相外切,且与直线l相切.设动圆圆心P的轨迹为E.
(1)求E的方程;
(2)若点A,B是E上的两个动点,O为坐标原点,且![]() ,求证:直线AB恒过定点.
,求证:直线AB恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,则下列说法错误的是( )
上的动点,则下列说法错误的是( )
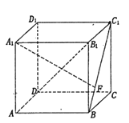
A. 当点![]() 移动至
移动至![]() 中点时,直线
中点时,直线![]() 与平面
与平面![]() 所成角最大且为
所成角最大且为![]()
B. 无论点![]() 在
在![]() 上怎么移动,都有
上怎么移动,都有![]()
C. 当点![]() 移动至
移动至![]() 中点时,才有
中点时,才有![]() 与
与![]() 相交于一点,记为点
相交于一点,记为点![]() ,且
,且![]()
D. 无论点![]() 在
在![]() 上怎么移动,异面直线
上怎么移动,异面直线![]() 与
与![]() 所成角都不可能是
所成角都不可能是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面![]() 与平面
与平面![]() 平行的充分条件可以是( )
平行的充分条件可以是( )
A.![]() 内有无穷多条直线都与
内有无穷多条直线都与![]() 平行
平行
B.直线![]() ,
,![]() ,且直线a不在
,且直线a不在![]() 内,也不在
内,也不在![]() 内
内
C.直线![]() ,直线
,直线![]() ,且
,且![]() ,
,![]()
D.![]() 内的任何一条直线都与
内的任何一条直线都与![]() 平行
平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快餐连锁店招聘外卖骑手,该快餐连锁店提供了两种日工资方案:方案①:规定每日底薪50元,快递业务每完成一单提成3元;方案②:规定每日底薪100元,快递业务的前44单没有提成,从第45单开始,每完成一单提成5元.该快餐连锁店记录了每天骑手的人均业务量.现随机抽取100天的数据,将样本数据分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 七组,整理得到如图所示的频率分布直方图.
七组,整理得到如图所示的频率分布直方图.
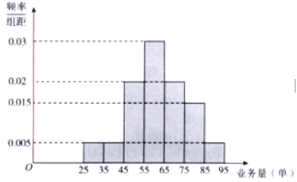
(1)随机选取一天,估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率;
(2)若骑手甲、乙选择了日工资方案①,丙、丁选择了日工资方案②.现从上述4名骑手中随机选取2人,求至少有1名骑手选择方案①的概率;
(3)若从人均日收入的角度考虑,请你利用所学的统计学知识为新聘骑手做出日工资方案的选择,并说明理由.(同组中的每个数据用该组区间的中点值代替)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若函数![]() 在区间
在区间![]() 内恰有一个零点,求
内恰有一个零点,求![]() 的取值范围;
的取值范围;
(3)设![]() ,当函数
,当函数![]() 的定义域为
的定义域为![]() 时,值域为
时,值域为![]() ,求a,b的值.
,求a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com