
(文)要将甲、乙两种大小不同的钢板截成A、B两种规格,每张钢板可同时截得A、B两种规格的小钢板的块数如下表所示:
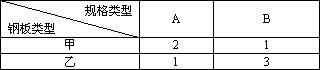
已知库房中现有甲、乙两种钢板的数量分别为5张和10张,市场急需A、B两种规格的成品数分别为15块和27块.
(1)问各截这两种钢板多少张可得到所需的成品数,且使所用的钢板张数最少?
(2)若某人对线性规划知识了解不多,而在可行域的整点中随意取出一解,求其恰好取到最优解的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com