
【题目】一幅标准的三角板如图(1)中,![]() 为直角,
为直角,![]() ,
,![]() 为直角,
为直角,![]() ,且
,且![]() ,把
,把![]() 与
与![]() 拼齐使两块三角板不共面,连结
拼齐使两块三角板不共面,连结![]() 如图(2).
如图(2).
(1)若![]() 是
是![]() 的中点,求证:
的中点,求证:![]() ;
;
(2)在《九章算术》中,称四个面都是直角三角形的三棱锥为“鳖臑”,若图(2)中![]() ,三棱锥
,三棱锥![]() 的体积为
的体积为![]() ,则图(2)是否为鳖臑?说明理由.
,则图(2)是否为鳖臑?说明理由.

科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() ,
,![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 在
在![]() 处的切线平行于
处的切线平行于![]() 轴,是否存在整数
轴,是否存在整数![]() ,使不等式
,使不等式![]() 在
在![]() 时恒成立?若存在,求出
时恒成立?若存在,求出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.

(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求二面角A1-BC1-B1的余弦值;
(Ⅲ)证明:在线段BC1存在点D,使得AD⊥A1B,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市理论预测2020年到2024年人口总数与年份的关系如下表所示:
年份202x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请在右面的坐标系中画出上表数据的散点图;

(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(3)据此估计2025年该城市人口总数.
(参考公式: ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
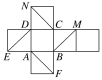
【题目】 如图是正方体的平面展开图.在这个正方体中,
①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.
以上四个命题中,正确命题的序号是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com