
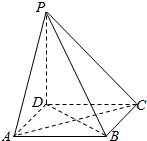
 如图,四棱锥P-ABCD的各棱长都为a.
如图,四棱锥P-ABCD的各棱长都为a.分析 (1)根据题意得出四边形ABCD是菱形,$\overrightarrow{BD}$⊥$\overrightarrow{OC}$;△PBD是等腰三角形,$\overrightarrow{PO}$⊥$\overrightarrow{BD}$;
利用平面向量的数量积求出$\overrightarrow{BD}$⊥$\overrightarrow{PC}$=0,即证BD⊥PC;
(2)根据题意,利用Rt△POC,求出<$\overrightarrow{AC}$,$\overrightarrow{PC}$>的大小,再求模长|$\overrightarrow{AC}$+$\overrightarrow{PC}$|.
解答  解:(1)证明:设AC、BD交于点O,连接PO,如图所示;
解:(1)证明:设AC、BD交于点O,连接PO,如图所示;
四棱锥P-ABCD中,AB=BC=CD=DA=a,
∴四边形ABCD是菱形,
∴BD⊥AC,且OA=OC;
即$\overrightarrow{BD}$⊥$\overrightarrow{OC}$,$\overrightarrow{BD}$•$\overrightarrow{OC}$=0;
又PB=PD=a,
∴PO⊥BD,
即$\overrightarrow{PO}$⊥$\overrightarrow{BD}$,$\overrightarrow{BD}$•$\overrightarrow{PO}$=0,;
∴$\overrightarrow{BD}$•($\overrightarrow{PO}$+$\overrightarrow{OC}$)=0,
即$\overrightarrow{BD}$•$\overrightarrow{PC}$=0,
∴$\overrightarrow{BD}$⊥$\overrightarrow{PC}$=0,即BD⊥PC;
(2)根据题意,四棱锥P-ABCD是棱长相等的正四棱锥,且AB=a,
∴顶点P在底面的射影是正方形ABCD的中心O,
在Rt△POC中,PC=a,OC=$\frac{\sqrt{2}}{2}$a,
∴OP=OC=$\frac{\sqrt{2}}{2}$a,
∴∠ACP=<$\overrightarrow{CP}$,$\overrightarrow{CA}$>=<$\overrightarrow{AC}$,$\overrightarrow{PC}$>=$\frac{π}{4}$,
∴${(\overrightarrow{AC}+\overrightarrow{PC})}^{2}$=${\overrightarrow{AC}}^{2}$+2$\overrightarrow{AC}$•$\overrightarrow{PC}$+${\overrightarrow{PC}}^{2}$=${(\sqrt{2}a)}^{2}$+2×$\sqrt{2}$a×a×cos$\frac{π}{4}$+a2=5a2;
∴|$\overrightarrow{AC}$+$\overrightarrow{PC}$|=$\sqrt{5}$a.
点评 本题考查了空间向量的应用问题,也考查了数形结合的数学思想,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | {x|-3≤x<0} | B. | {x|-2≤x<0} | C. | {x|-3<x<0} | D. | {x|-2<x<0} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com