练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知定义在上的函数满足：，且，则方程在区间上的所有实根之和为( )

    A. B. C. D.

    【答案】A

    【解析】

    将方程根的问题转化为函数图象的交点问题，将函数式化简，根据图象的对称性，由图象观察即可．

    ∵f（x）=，且f（x+2）=f（x），

    ∴f（x﹣2）﹣3=

    又g（x）=，则g（x）=3，

    ∴g（x﹣2）﹣3=，

    上述两个函数都是关于（﹣2，3）对称，

    由图象可得：y=f（x）和y=g（x）的图象在区间[﹣5，1]上有4个交点，

    它们都关于点（﹣2，3）对称，故之和为﹣2×4=﹣8．

    但由于（﹣1，4）取不到，故之和为﹣8+1=﹣7．

    即方程f（x）=g（x）在区间[﹣5，1]上的实根有3个，

    故方程f（x）=g（x）在区间[﹣8，3]上的所有实根之和为﹣7．

    故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图（1）在等腰直角三角形中，，将沿中位线翻折得到如图（2）所示的空间图形，使二面角的大小为.

    （1）求证：平面平面；

    （2）若，求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，函数.

    （1）经过原点分别作曲线、的切线，若两切线的斜率互为倒数，证明：；

    （2）设，当时，恒成立，试求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将各位数字和为8的全体正整数按自小到大的顺序排成一个数列，称为P数列.则2015为其中第________项.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂生产某种产品的年固定成本为200万元，每生产千件，需另投入成本为，当年产量不足80千件时，（万元）．当年产量不小于80千件时，（万元）．每件商品售价为0.05万元．通过市场分析，该厂生产的商品能全部售完．

    （1）写出年利润（万元）关于年产量（千件）的函数解析式；

    （2）当年产量为多少千件时，该厂在这一商品的生产中所获利润最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，且过点.

    （1）求椭圆C的标准方程；

    （2）点P是椭圆上异于短轴端点A，B的任意一点，过点P作轴于Q，线段PQ的中点为M.直线AM与直线交于点N，D为线段BN的中点，设O为坐标原点，试判断以OD为直径的圆与点M的位置关系.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

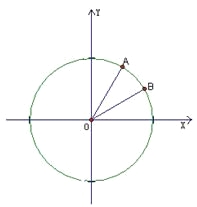
    【题目】如图，在平面直角坐标系中，以轴为始边做两个锐角，它们的终边分别与单位圆相交于A，B两点，已知A，B的横坐标分别为

    （1）求的值； （2）求的值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】把编号为1，2，3，4的四个大小、形状相同的小球，随机放入编号为1，2，3，4的四个盒子里．每个盒子里放入一个小球．

    （1）求恰有两个球的编号与盒子的编号相同的概率；

    （2）设小球的编号与盒子编号相同的情况有种，求随机变量的分布列与期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数(其中为常数且)在处取得极值.

    (1)当时，求的极大值点和极小值点；

    (2)若在上的最大值为1，求的值.

    查看答案和解析>>

    同步练习册答案