【题目】如图，直三棱柱ABC﹣A1B1C1中，侧棱AA1⊥平面ABC．若AB=AC=AA1=1，BC= 
，则异面直线A1C与B1C1所成的角为（ ） 
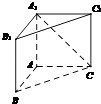
A.30°
B.45°
C.60°
D.90°
【答案】C
【解析】解：因为几何体是棱柱，BC∥B1C1，则直线A1C与BC所成的角为就是异面直线A1C与B1C1所成的角．
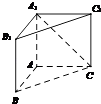
直三棱柱ABC﹣A1B1C1中，侧棱AA1⊥平面ABC．若AB=AC=AA1=1，BC= 
，BA1= 
，CA1= 
，
三角形BCA1是正三角形，异面直线所成角为60°．
故选：C．
【考点精析】关于本题考查的异面直线及其所成的角，需要了解异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系才能得出正确答案．
科目：高中数学 来源： 题型：
【题目】已知椭圆 
（a＞0，b＞0）上的点P到左、右两焦点F1 ， F2的距离之和为2 
，离心率为 
．
（1）求椭圆的方程；
（2）是否存在同时满足①②两个条件的直线l？
①过点M（0， 
）；
②存在椭圆上与右焦点F2共线的两点A、B，且A、B关于直线l对称．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知实数p：x2﹣4x﹣12≤0，q：（x﹣m）（x﹣m﹣1）≤0
（1）若m=2，那么p是q的什么条件；
（2）若q是p的充分不必要条件，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直三棱柱ABC﹣A1B1C1中，∠ACB=90°，AC=BC=AA1=2，D、E分别为棱AB、BC的中点，点F在棱AA1上． 
（1）证明：直线A1C1∥平面FDE；
（2）若F为棱AA1的中点，求三棱锥A1﹣DEF的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=ln（a﹣ 
）（a∈R）．若关于x的方程ln[（4﹣a）x+2a﹣5]﹣f（x）=0的解集中恰好有一个元素，则实数a的取值范围为 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱锥S﹣ABC中，E为棱SC的中点，若AC=2 
，SA=SB=AB=BC=SC=2，则异面直线AC与BE所成的角为（ ）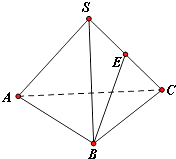 
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
