
【题目】已知集合A={x|2-a≤x≤2+a},B={x|x≤1或x≥4}.
(1)当a=3时,求A∩B;
(2)若a>0,且A∩B=![]() ,求实数a的取值范围.
,求实数a的取值范围.
科目:高中数学 来源: 题型:
【题目】某医药研究所开发一种新药,在试验药效时发现:如果成人按规定剂量服用,那么服药后每毫升血液中的含药量y(微克)与时间x(小时)之间满足y= 其对应曲线(如图所示)过点
其对应曲线(如图所示)过点![]() .
.

(1)试求药量峰值(y的最大值)与达峰时间(y取最大值时对应的x值);
(2)如果每毫升血液中含药量不少于1微克时治疗疾病有效,那么成人按规定剂量服用该药后一次能维持多长的有效时间(精确到0.01小时)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若存在x0∈R,使得f(x0)=x0成立,则称x0为f(x)的天宫一号点.已知函数f(x)=ax2+(b-7)x+18的两个天宫一号点分别是-3和2.
(1)求a,b的值及f(x)的表达式;
(2)当函数f(x)的定义域是[t,t+1]时,求函数f(x)的最大值g(t).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产的某种时令商品每件成本为![]() 元,经过市场调研发现,这种商品在未来
元,经过市场调研发现,这种商品在未来![]() 天内的日销售量
天内的日销售量![]() (件)与时间
(件)与时间![]() (天)的关系如下表所示.
(天)的关系如下表所示.
时间 | 1 | 3 | 6 | 10 | 36 | …… |
日销售量
| 94 | 90 | 84 | 76 | 24 | …… |
未来40天内,前20天每天的价格![]() (元/件)与时间
(元/件)与时间![]() (天)的函数关系式为
(天)的函数关系式为 ![]() ,且
,且![]() 为整数),后20天每天的价格
为整数),后20天每天的价格![]() (元/件)与时间
(元/件)与时间![]() (天)的函数关系式为
(天)的函数关系式为![]() ,且
,且![]() 为整数).
为整数).
(Ⅰ)认真分析表格中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据![]() (件)与
(件)与 ![]() (天)的关系式;
(天)的关系式;
(Ⅱ)试预测未来 40 天中哪一天的日销售利润最大,最大利润是多少?
(Ⅲ)在实际销售的前 20 天中,该公司决定每销售 1 件商品就捐赠![]() 元利润
元利润![]() 给希望工程. 公司通过销售记录发现,前 20 天中,每天扣除捐赠后的日销售利润随时间
给希望工程. 公司通过销售记录发现,前 20 天中,每天扣除捐赠后的日销售利润随时间![]() (天)的增大而增大,求
(天)的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为(-3,3),
满足f(-x)=-f(x),且对任意x,y,都有f(x)-f(y)=f(x-y),当x<0时,f(x)>0,f(1)=-2.
(1)求f(2)的值;
(2)判断f(x)的单调性,并证明;
(3)若函数g(x)=f(x-1)+f(3-2x),求不等式g(x)≤0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
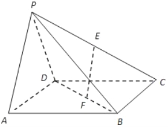
【题目】在四棱锥中![]() ,底面
,底面![]() 是正方形,侧面
是正方形,侧面![]() 底面
底面![]() ,且
,且![]() ,分别为
,分别为![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ,若存在,请求出点
,若存在,请求出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com