【题目】若函数
在定义域A上的值域为
,则区间A不可能为( )
A.
B.
C.
D.
【答案】D
【解析】
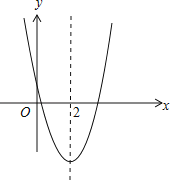
根据函数图象得到函数在R上的单调性是先减后增，再根据单调性分别求出选项中四个区间上的最大最小值，得到相应的值域，再与[﹣3，1]比较，即可得到正确选项．
∵函数f（x）＝x2﹣4x+1的图象是开口向上的抛物线，以x＝2为对称轴，
∴函数在区间（﹣∞，2）上为减函数，[2，+∞）上为增函数．
当x∈[0，4]时，函数最小值为f（2）＝﹣3，最大值为f（0）＝f（4）＝1，得函数值域为[﹣3，1]；
当x∈[2，4]时，函数最小值为f（2）＝﹣3，最大值为f（4）＝1，得函数值域为[﹣3，1]；
当x∈[1，4]时，函数最小值为f（2）＝﹣3，
∵f（1）＝﹣2＜f（4）＝1，∴最大值为f（4）＝1，得函数值域为[﹣3，1]；
当x∈[﹣3，5]时，最小值f（2）＝﹣3，最大值为f（﹣3）＝22，得函数值域为[﹣2，22]．
根据以上的讨论可得区间A不可能为[﹣3，5]．
故选：D．
新课标阶梯阅读训练系列答案科目：高中数学 来源： 题型：
【题目】已知函数y=f(x)是定义在R上的奇函数,且当x≥0时,f(x)=-x2+ax.
(1)若a=-2,求函数f(x)的解析式;
(2)若函数f(x)为R上的单调减函数,
①求a的取值范围;
②若对任意实数m,f(m-1)+f(m2+t)<0恒成立,求实数t的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四面体ABCD中，△ABC是等边三角形，平面ABC⊥平面ABD，点M为棱AB的中点，AB=2，AD=
，∠BAD=90°．
（Ⅰ）求证：AD⊥BC；
（Ⅱ）求异面直线BC与MD所成角的余弦值；
（Ⅲ）求直线CD与平面ABD所成角的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知下列说法：
①命题“x0∈R，x＋1＞3x0”的否定是“x∈R，x2＋1＜3x”；
②已知p，q为两个命题，若“p∨q”为假命题，则“￢p∧￢q”为真命题
③“a＞2”是“a＞5”的充分不必要条件
④“若xy＝0，则x＝0且y＝0”的逆否命题为真命题
其中正确说法的个数为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，如果存在给定的实数对
，使得
恒成立，则称为“
函数”.
（1）判断函数
，
是否是“函数”；
（2）若
是一个“函数”，求出所有满足条件的有序实数对；
（3）若定义域为
的函数是“
-函数”，且存在满足条件的有序实数对
和
，当
时，的值域为
，求当
时函数的值域.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝b·ax(其中a，b为常量，且a>0，a≠1)的图象经过点A(1,6)，B(3,24)．
(1)求f(x)；
(2)若不等式(
)x＋(
)x－m≥0在x∈(－∞，1]时恒成立，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，从一个面积为
的半圆形铁皮上截取两个高度均为
的矩形，并将截得的两块矩形铁皮分别以
，
为母线卷成两个高均为的圆柱（无底面，连接部分材料损失忽略不计）．记这两个圆柱的体积之和为
．
（1）将表示成的函数关系式，并写出的取值范围；
（2）求两个圆柱体积之和的最大值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
