
 中
中 ,
, 平面
平面 ,
, ,
, ,
, .
.

 ;
; 在棱
在棱 上,
上, ,若
,若 ∥平面
∥平面 ,求
,求 的值.
的值.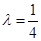 。
。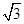 ,∴BD=2,∠ABD=30°,
,∴BD=2,∠ABD=30°,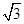 ,
,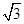 ,0),P(0,0,a)C、(-3,
,0),P(0,0,a)C、(-3,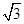 ,0),
,0),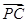 =(-3,
=(-3,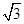 ,-a),
,-a),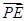 =(-3λ,
=(-3λ,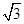 λ,-aλ),
λ,-aλ),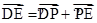 =(0,0,a)+(-3λ,
=(0,0,a)+(-3λ,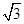 λ,-aλ)=(-3λ,
λ,-aλ)=(-3λ,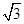 λ,a-aλ),
λ,a-aλ), =(0,
=(0,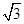 ,0),
,0),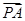 =(1,0,-a),
=(1,0,-a),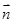 =(x,y,z)为面PAB的法向量,由
=(x,y,z)为面PAB的法向量,由 ·
·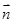 =0,
=0,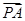 ·
·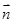 =0,得x-az=0,取x=a,z=1,
=0,得x-az=0,取x=a,z=1,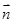 =(a,0,1),
=(a,0,1),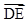 ⊥
⊥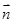
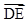 ·
·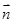 =0,-3aλ+a-aλ=0,∴λ=
=0,-3aλ+a-aλ=0,∴λ=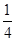 。
。

科目:高中数学 来源:不详 题型:解答题
 ,下半部分是长方体
,下半部分是长方体 。图2、图3分别是该标识墩的正(主)视图和俯视图。
。图2、图3分别是该标识墩的正(主)视图和俯视图。
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 轴上有一条单位长度的线段
轴上有一条单位长度的线段 ,沿着与其垂直的
,沿着与其垂直的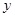 轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形
轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形 ),再把正方形沿着与其所在的平面垂直的
),再把正方形沿着与其所在的平面垂直的 轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体
轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体 )。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有
)。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有 个顶点,
个顶点, 条棱,
条棱, 个面,则
个面,则 的值分别为 ( )
的值分别为 ( )
A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com