
【题目】设点![]() ,动圆
,动圆![]() 经过点
经过点![]() 且和直线
且和直线![]() 相切,记动圆的圆心
相切,记动圆的圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设曲线![]() 上一点
上一点![]() 的横坐标为
的横坐标为![]() ,过
,过![]() 的直线交
的直线交![]() 于一点
于一点![]() ,交
,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于另一点
于另一点![]() ,若
,若![]() 是
是![]() 的切线,求
的切线,求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)先利用抛物线的定义判定动点轨迹是一个抛物线,再利用待定系数法求出抛物线的方程;(2)设出直线方程,联立直线和抛物线的方程,得到关于![]() 的一元二次方程,利用根与系数的关系和导数的几何意义进行求解.
的一元二次方程,利用根与系数的关系和导数的几何意义进行求解.
试题解析:(1)过点![]() 作直线
作直线![]() 垂直于直线
垂直于直线![]() 于点
于点![]() ,由题意得
,由题意得![]() ,所以动点
,所以动点![]() 的轨迹是以
的轨迹是以![]() 为焦点,直线
为焦点,直线![]() 为准线的抛物线.所以抛物线
为准线的抛物线.所以抛物线![]() 得方程为
得方程为![]() .
.
(2)由题意知,过点![]() 的直线
的直线![]() 斜率存在且不为
斜率存在且不为![]() ,设其为
,设其为![]() ,则
,则![]() ,当
,当![]() ,则
,则 .联立方程
.联立方程![]() ,整理得:
,整理得: ![]() .即
.即![]() ,解得
,解得![]() 或
或![]() ,
, ![]() ,而
,而![]() ,所以直线
,所以直线![]() 斜率为
斜率为![]() ,
, ![]() ,联立方程
,联立方程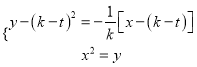 ,整理得:
,整理得: ![]() ,即
,即![]() ,解得
,解得![]() ,或
,或![]() .
.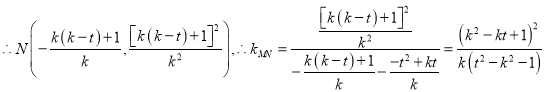 .
.
而抛物线在点![]() 的切线斜率,
的切线斜率, ![]()
![]() ,
, ![]() 是抛物线的切线,
是抛物线的切线, 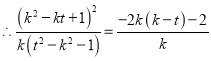 ,整理得
,整理得![]() ,解得
,解得![]() (舍去),或
(舍去),或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组.现要从中抽取10名学生,各组内抽取的编号按依次增加10进行系统抽样.
(1)若抽出的一个号码为22,则此号码所在的组数是多少?据此写出所有被抽出学生的号码;
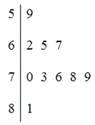
(2)分别统计这10名学生的数学成绩,获得成绩数据的茎叶图如图4所示,求该样本的方差;
(3)在(2)的条件下,从这10名学生中随机抽取两名成绩不低于73分的学生,求被抽取到的两名学生的成绩之和不小于154分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,侧面
中,侧面![]() 是边长为2的菱形,且
是边长为2的菱形,且![]() ,
, ![]() ,四棱锥
,四棱锥![]() 的体积为2,点
的体积为2,点![]() 在平面
在平面![]() 内的正投影为
内的正投影为![]() ,且
,且![]() 在
在![]() 上,点
上,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
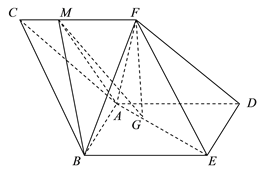
(Ⅰ)证明:直线![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,且
,且![]() 与椭圆
与椭圆![]() 只有一个公共点
只有一个公共点![]() .
.
①求证: ![]() ;
;
②当![]() 为何值时,
为何值时, ![]() 取得最大值?并求出最大值.
取得最大值?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆心为
,圆心为![]() ,定点
,定点![]() ,
, ![]() 为圆
为圆![]() 上一点,线段
上一点,线段![]() 上一点
上一点![]() 满足
满足![]() ,直线
,直线![]() 上一点
上一点![]() ,满足
,满足![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)![]() 为坐标原点,
为坐标原点, ![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与
与![]() 相切,并与轨迹
相切,并与轨迹![]() 交于不同的两点
交于不同的两点![]() .当
.当![]() 且满足
且满足![]() 时,求
时,求![]() 面积
面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家举行大型的促销活动,经测算某产品当促销费用为![]() 万元时,销售量
万元时,销售量![]() 万件满足
万件满足![]() (其中
(其中![]() ,
, ![]() 为正常数),现假定生产量与销售量相等,已知生产该产品
为正常数),现假定生产量与销售量相等,已知生产该产品![]() 万件还需投入成本
万件还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 万元/万件.
万元/万件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,等边三角形![]() 的边长为
的边长为![]() ,且其
,且其
三个顶点均在抛物线![]() 上.
上.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)设动直线![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() ,与直线
,与直线![]()
相交于点![]() .证明以
.证明以![]() 为直径的圆恒过
为直径的圆恒过![]() 轴上某定点.
轴上某定点.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在平面直角坐标系xOy 中,曲线C的参数方程为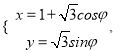 (
(![]() 是参数,0≤
是参数,0≤![]() ≤π),以O 为极点,以x 轴的正半轴为极轴,建立极坐标系.
≤π),以O 为极点,以x 轴的正半轴为极轴,建立极坐标系.
(Ⅰ)求曲线C 的极坐标方程;
(Ⅱ)直线l1,的极坐标方程是2psin(θ+![]() )+
)+![]() =0,直线l2:θ =
=0,直线l2:θ =![]() 与曲线C的交点为P,与直线l1的交点为Q,求线段PQ的长.
与曲线C的交点为P,与直线l1的交点为Q,求线段PQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com