
【题目】已知函数f(x)=|x﹣1|+|x﹣a|.
(1)若a=﹣1,解不等式f(x)≥3;
(2)如果x∈R,使得f(x)<2成立,求实数a的取值范围.
【答案】
(1)解:若a=﹣1,f(x)≥3,
即为|x﹣1|+|x+1|≥3,
当x≤﹣1时,1﹣x﹣x﹣1≥3,即有x≤﹣ ![]() ;
;
当﹣1<x<1时,1﹣x+x+1=2≥3不成立;
当x≥1时,x﹣1+x+1=2x≥3,解得x≥ ![]() .
.
综上可得,f(x)≥3的解集为(﹣∞,﹣ ![]() ]∪[
]∪[ ![]() ,+∞)
,+∞)
(2)解:x∈R,使得f(x)<2成立,
即有2>f(x)min,
由函数f(x)=|x﹣1|+|x﹣a|≥|x﹣1﹣x+a|=|a﹣1|,
当(x﹣1)(x﹣a)≤0时,取得最小值|a﹣1|,
则|a﹣1|<2,
即﹣2<a﹣1<2,
解得﹣1<a<3.
则实数a的取值范围为(﹣1,3)
【解析】(1)由题意可得|x﹣1|+|x+1|≥3,讨论当x≤﹣1时,当﹣1<x<1时,当x≥1时,去掉绝对值解不等式,最后求并集;(2)由题意可得2>f(x)min , 运用绝对值不等式的性质,可得f(x)的最小值,再由绝对值不等式的解法,可得a的范围.
【考点精析】掌握绝对值不等式的解法是解答本题的根本,需要知道含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】以下四个命题,其中正确的个数有( )
①由独立性检验可知,有![]() 的把握认为物理成绩与数学成绩有关,某人数学成绩优秀,则他有99%的可能物理优秀.
的把握认为物理成绩与数学成绩有关,某人数学成绩优秀,则他有99%的可能物理优秀.
②两个随机变量相关性越强,则相关系数的绝对值越接近于1;
③在线性回归方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加0.2个单位;
平均增加0.2个单位;
④对分类变量![]() 与
与![]() ,它们的随机变量
,它们的随机变量![]() 的观测值
的观测值![]() 来说,
来说, ![]() 越小,“
越小,“![]() 与
与![]() 有关系”的把握程度越大.
有关系”的把握程度越大.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数![]() 与听课时间
与听课时间![]() (单位:分钟)之间的关系满足如图所示的曲线.当
(单位:分钟)之间的关系满足如图所示的曲线.当![]() 时,曲线是二次函数图象的一部分,当
时,曲线是二次函数图象的一部分,当![]() 时,曲线是函数
时,曲线是函数![]() 图象的一部分.根据专家研究,当注意力指数
图象的一部分.根据专家研究,当注意力指数![]() 大于80时学习效果最佳.
大于80时学习效果最佳.

(1)试求![]() 的函数关系式;
的函数关系式;
(2)教师在什么时段内安排核心内容,能使得学生学习效果最佳?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若在区间![]() 上存在不相等的实数
上存在不相等的实数![]() ,使
,使![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)若函数![]() 有两个不同的极值点
有两个不同的极值点![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,且经过点
,且经过点![]() ,直线
,直线![]() 交椭圆于不同的两点
交椭圆于不同的两点![]() .
.
(1)求椭圆的方程;
(2)求![]() 的取值范围;
的取值范围;
(3)若直线![]() 不过点
不过点![]() ,求证:直线
,求证:直线![]() 的斜率互为相反数.
的斜率互为相反数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=2sin(ωx+ ![]() )(ω>0)的图象向右平移
)(ω>0)的图象向右平移 ![]() 个单位,得到函数y=g(x)的图象,若y=g(x)在[﹣
个单位,得到函数y=g(x)的图象,若y=g(x)在[﹣ ![]() ,
, ![]() ]上为增函数,则ω的最大值为( )
]上为增函数,则ω的最大值为( )
A.3
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中错误的是( )
A.设命题p:?x∈R,使![]() +x+2<0,则¬P:?x∈R,都有
+x+2<0,则¬P:?x∈R,都有![]() +x+2≥0
+x+2≥0
B.若x,y∈R,则“x=y”是“xy≤![]() 取到等号”的充要条件
取到等号”的充要条件
C.已知命题p和q,若p∧q为假命题,则命题p与q都为假命题
D.命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
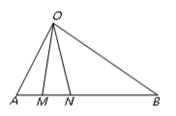
【题目】如图所示,某公路![]() 一侧有一块空地
一侧有一块空地![]() ,其中
,其中 ![]() ,
,![]() .当地政府拟在中间开挖一个人工湖△OMN,其中M,N都在边AB上(M,N不与A,B重合,M在A,N之间),且∠MON=30°.
.当地政府拟在中间开挖一个人工湖△OMN,其中M,N都在边AB上(M,N不与A,B重合,M在A,N之间),且∠MON=30°.
(1)若M在距离A点2 km处,求点M,N之间的距离;
(2)为节省投入资金,人工湖△OMN的面积要尽可能小.试确定M的位置,使△OMN的面积最小,并求出最小面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com