
【题目】如图,一块黄铜板上插着三根宝石针,在其中一根针上从下到上穿好由大到小的若干金片.若按照下面的法则移动这些金片:每次只能移动一片金片;每次移动的金片必须套在某根针上;大片不能叠在小片上面.设移完n片金片总共需要的次数为an,可推得a1=1,an+1=2an+1.如图是求移动次数在1000次以上的最小片数的程序框图模型,则输出的结果是( )

A. 8B. 9C. 10D. 11
科目:高中数学 来源: 题型:
【题目】如图,圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,与
,与![]() 轴正半轴交于两点
轴正半轴交于两点![]() ,
,![]() (
(![]() 在
在![]() 的上方),且
的上方),且![]() .
.
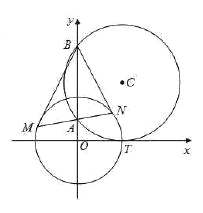
(1)求圆![]() 的标准方程;
的标准方程;
(2)过点![]() 作任一条直线与圆
作任一条直线与圆![]() :
:![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
①求证:![]() 为定值,并求出这个定值;
为定值,并求出这个定值;
②求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机厂商推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下:
女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 20 | 40 | 80 | 50 | 10 | |
男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 45 | 75 | 90 | 60 | 30 |
(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的波动大小(不计算具体值,给出结论即可);

(2)把评分不低于70分的用户称为“评分良好用户”,能否有![]() 的把握认为“评分良好用户”与性别有关?
的把握认为“评分良好用户”与性别有关?
参考附表:
|
|
|
| |
|
|
|
|
|
参考公式 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的机器上存在一种易损元件,这种元件发生损坏时,需要及时维修. 现有甲、乙两名工人同时从事这项工作,下表记录了某月1日到10日甲、乙两名工人分别维修这种元件的件数.
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 | 8日 | 9日 | 10日 |
甲维修的元件数 | 3 | 5 | 4 | 6 | 4 | 6 | 3 | 7 | 8 | 4 |
乙维修的元件数 | 4 | 7 | 4 | 5 | 5 | 4 | 5 | 5 | 4 | 7 |
(1)从这![]() 天中,随机选取一天,求甲维修的元件数不少于5件的概率;
天中,随机选取一天,求甲维修的元件数不少于5件的概率;
(2)试比较这10天中甲维修的元件数的方差![]() 与乙维修的元件数的方差
与乙维修的元件数的方差![]() 的大小.(只需写出结论);
的大小.(只需写出结论);
(3)由于甲、乙的任务量大,拟增加工人,为使增加工人后平均每人每天维修的元件不超过3件,请利用上表数据估计最少需要增加几名工人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com