已知a≥0,函数f(x)=(x2-2ax)ex.
(Ⅰ)当x为何值时,f(x)取得最小值?证明你的结论;
(Ⅱ)设f(x)在[-1,1]上是单调函数,求a的取值范围.
解:(1)令f'(x)=0即[x
2-2(a-1)x-2a]e
x=0∴x
2-2(a-1)x-2a=0
∵△=[2(a-1)]
2+8a=4(a
2+1)>0∴x
1=a-1-

,x
2=a-1+

又∵当x∈(-∞,a-1-

)时,f'(x)>0;
当x∈(a-1-

,a-1+

)时,f'(x)<0;
当x∈(a-1+

,+∞)时,f'(x)>0.
列表如下:

∴x
1,x
2分别为f(x)的极大值与极小值点.
又∵
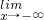
f(x)=0;当x→+∞时,f(x)→+∞.
而f(a-1+

)=2(1-

)
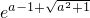
<0.
∴当x=a-1+

时,f(x)取得最小值.
(2)f(x)在[-1,1]上单调,则f'(x)≥0(或≤0)在[-1,1]上恒成立.
而f'(x)=[x
2-2(a-1)x-2a]e
x,令g(x)=x
2-2(a-1)x-2a=[x-(a-1)]
2-(a
2+1).
∴f'(x)≥0(或≤0)即g(x)≥0(或≤0).
当g(x)≥0在[-1,1]上恒成立时,有
①当-1≤a-1≤1即0≤a≤2时,g(x)
min=g(a-1)=-(a
2+1)≥0(舍);
②当a-1>1即a≥2时,g(x)
min=g(1)=3-4a≥0∴a≤

(舍).
当g(x)≤0在[-1,1]上恒成立时,有
①当-1≤a-1≤0即0≤a≤1时,g(x)
max=g(1)=3-4a≤0,∴

≤a≤1;
②当0<a-1≤1即1<a≤2时,g(x)
max=g(-1)=-1≤0,∴1<a≤2;
③当1<a-1即a>2时,g(x)
max=g(-1)=-1≤0,∴a>2.
故a∈[

,+∞).
分析:(Ⅰ)直接求两个函数乘积的导函数,令其等于0,求出极值点,判断单调性,进而求出最小值;
(Ⅱ)f(x)在[-1,1]上是单调函数,即其导函数恒大于等于或小于等于零,转化为不等式恒成立问题,再通过构造函数转化为求函数最值,利用导数的方法即可解决.
点评:本题考查函数单调性的性质,导数在函数最大值、最小值中的应用,灵活运用分类讨论思想与转化思想是解决此类题目的关键,属于中档题.

 ,x2=a-1+
,x2=a-1+
 )时,f'(x)>0;
)时,f'(x)>0; ,a-1+
,a-1+ )时,f'(x)<0;
)时,f'(x)<0; ,+∞)时,f'(x)>0.
,+∞)时,f'(x)>0.
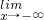 f(x)=0;当x→+∞时,f(x)→+∞.
f(x)=0;当x→+∞时,f(x)→+∞. )=2(1-
)=2(1- )
)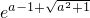 <0.
<0. 时,f(x)取得最小值.
时,f(x)取得最小值. (舍).
(舍). ≤a≤1;
≤a≤1; ,+∞).
,+∞).
