
分析 (1)运用向量的数量积的坐标表示,结合同角三角函数的基本关系式,化简计算即可得到所求值;
(2)运用向量共线坐标表示,求得tanθ=2,再由二倍角公式和两角和的正弦公式,计算即可得到所求值.
解答 解:(1)由向量$\overrightarrow{a}$=(2,sinθ),$\overrightarrow{b}$=(1,cosθ),θ∈(0,$\frac{π}{2}$),
可得$\overrightarrow{a}$$•\overrightarrow{b}$=2+sinθcosθ=$\frac{7}{3}$,
即sinθcosθ=$\frac{7}{3}$-2=$\frac{1}{3}$,
则sinθ+cosθ=$\sqrt{(sinθ+cosθ)^{2}}$=$\sqrt{si{n}^{2}θ+co{s}^{2}θ+2sinθcosθ}$
=$\sqrt{1+\frac{2}{3}}$=$\frac{\sqrt{15}}{3}$;
(2)若$\overrightarrow{a}$∥$\overrightarrow{b}$,则2cosθ=sinθ,即tanθ=2,
sin2θ=2sinθcosθ=$\frac{2sinθcosθ}{si{n}^{2}θ+co{s}^{2}θ}$=$\frac{2tanθ}{1+ta{n}^{2}θ}$=$\frac{2×2}{1+{2}^{2}}$=$\frac{4}{5}$,
cos2θ=cos2θ-sin2θ=$\frac{co{s}^{2}θ-si{n}^{2}θ}{co{s}^{2}θ+si{n}^{2}θ}$=$\frac{1-ta{n}^{2}θ}{1+ta{n}^{2}θ}$=$\frac{1-4}{1+4}$=-$\frac{3}{5}$,
则sin(2θ+$\frac{π}{3}$)=sin2θcos$\frac{π}{3}$+cos2θsin$\frac{π}{3}$
=$\frac{4}{5}$×$\frac{1}{2}$+(-$\frac{3}{5}$)×$\frac{\sqrt{3}}{2}$=$\frac{4-3\sqrt{3}}{10}$.
点评 本题考查三角函数的求值,注意运用三角函数的恒等变换公式,同时考查向量的数量积和共线条件,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
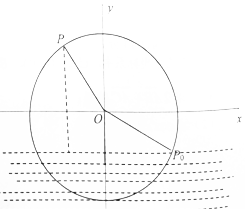 一半径为4米的水轮如图所示,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动5圈,如果当水轮上点P从水中浮现时(图象P0点)开始计算时间,且点P距离水面的高度f(t)(米)与时间t(秒)满足函数:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).
一半径为4米的水轮如图所示,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动5圈,如果当水轮上点P从水中浮现时(图象P0点)开始计算时间,且点P距离水面的高度f(t)(米)与时间t(秒)满足函数:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com