
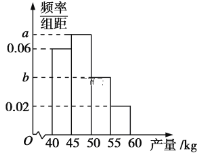
ЁОЬтФПЁПФГЙћХЉбЁШЁвЛЦЌЩНЕижжжВКьшжЃЌЪеЛёЪБЃЌИУЙћХЉЫцЛњбЁШЁЙћЪї20жъзїЮЊбљБОВтСПЫќУЧУПвЛжъЕФЙћЪЕВњСП(ЕЅЮЛЃКkg)ЃЌЛёЕУЕФЫљгаЪ§ОнАДееЧјМф(40,45]ЃЌ(45,50]ЃЌ(50,55]ЃЌ(55,60]НјааЗжзщЃЌЕУЕНЦЕТЪЗжВМжБЗНЭМШчЭМ.вбжЊбљБОжаВњСПдкЧјМф(45,50]ЩЯЕФЙћЪїжъЪ§ЪЧВњСПдкЧјМф(50,60]ЩЯЕФЙћЪїжъЪ§ЕФ![]() БЖ.
БЖ.
ЃЈ1ЃЉЧѓ![]() ЁЂ
ЁЂ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЧѓбљБОЕФЦНОљЪ§ЃЛ
ЃЈ3ЃЉДгбљБОжаВњСПдкЧјМф(50,60]ЩЯЕФЙћЪїРяЫцЛњГщШЁСНжъЃЌЧѓВњСПдкЧјМф(55,60]ЩЯЕФЙћЪїжСЩйгавЛжъБЛГщжаЕФИХТЪ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛ ЃЈ2ЃЉ48ЃЛ ЃЈ3ЃЉ
ЃЛ ЃЈ2ЃЉ48ЃЛ ЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁП
(1)ЗжЮібљБОжаВњСПдкЧјМф![]() КЭ
КЭ![]() ЩЯЕФЙћЪїЃЌдйНсКЯЦЕТЪЗжВМжБЗНЭМЕФЬиеїСЊСЂЗНГЬзщЧѓГіНсЙћ
ЩЯЕФЙћЪїЃЌдйНсКЯЦЕТЪЗжВМжБЗНЭМЕФЬиеїСЊСЂЗНГЬзщЧѓГіНсЙћ
(2)гЩЦЕТЪЗжВМжБЗНЭМШЁжаМфжЕРДМЦЫуГіЦНОљЪ§
(3)ЗжБ№МЦЫуГідкЧјМф![]() КЭ
КЭ![]() ЩЯЕФЙћЪїЪ§СПЃЌдЫгУИХТЪжЊЪЖЧѓГіНсЙћ
ЩЯЕФЙћЪїЪ§СПЃЌдЫгУИХТЪжЊЪЖЧѓГіНсЙћ
ЃЈ1ЃЉбљБОжаВњСПдкЧјМф(45,50]ЩЯЕФЙћЪїга![]() (жъ)ЃЌ
(жъ)ЃЌ
бљБОжаВњСПдкЧјМф(50,60]ЩЯЕФЙћЪїга![]() (жъ)
(жъ)
дђга![]() МД
МД![]() Ђй
Ђй
ИљОнЦЕТЪЗжВМжБЗНЭМПЩжЊ![]() Ђк
Ђк
НтЂйЂкзщГЩЕФЗНГЬзщЕУ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЦНОљЪ§![]()
![]() .
.
ЃЈ3ЃЉбљБОжаВњСПдкЧјМф(50,55]ЩЯЕФЙћЪїга![]() (жъ)ЃЌВњСПдкЧјМф(55,60]ЩЯЕФЙћЪїга
(жъ)ЃЌВњСПдкЧјМф(55,60]ЩЯЕФЙћЪїга![]() (жъ)
(жъ)
ЩшЁАДгбљБОжаВњСПдкЧјМф(50,60]ЩЯЕФЙћЪїРяЫцЛњГщШЁСНжъЃЌВњСПдкЧјМф(55,60]ЩЯЕФЙћЪїжСЩйгавЛжъБЛГщжаЁБЮЊЪТМў![]() ЃЌдђ
ЃЌдђ![]() .
.


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌвд
жаЃЌвд![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ![]() жсЗЧИКАыжсЮЊМЋжсНЈСЂзјБъЯЕЃЌвбжЊЧњЯп
жсЗЧИКАыжсЮЊМЋжсНЈСЂзјБъЯЕЃЌвбжЊЧњЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() ЕФВЮЪ§ЗНГЬЮЊ:
ЕФВЮЪ§ЗНГЬЮЊ: 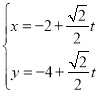 ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌСНЧњЯпЯрНЛгк
ЮЊВЮЪ§ЃЉЃЌСНЧњЯпЯрНЛгк![]() СНЕу.
СНЕу.
ЃЈ1ЃЉаДГіЧњЯп![]() ЕФжБНЧзјБъЗНГЬКЭжБЯп
ЕФжБНЧзјБъЗНГЬКЭжБЯп![]() ЕФЦеЭЈЗНГЬЃЛ
ЕФЦеЭЈЗНГЬЃЛ
ЃЈ2ЃЉШє![]() Чѓ
Чѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ![]() гы
гы![]() ОљЮЊСтаЮЃЌ
ОљЮЊСтаЮЃЌ ![]() ЃЌЧв
ЃЌЧв![]() .
.

ЃЈ1ЃЉЧѓжЄЃК ![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФе§ЯвжЕ.
ЫљГЩНЧЕФе§ЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩш![]() ЃЌЖЈвх
ЃЌЖЈвх![]() ЃЈ
ЃЈ![]() ЃЌЧв
ЃЌЧв![]() ЮЊГЃЪ§ЃЉЃЌШє
ЮЊГЃЪ§ЃЉЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎвдЯТЫФИіУќЬтжаЮЊецУќЬтЕФЪЧ__________.
ЃЎвдЯТЫФИіУќЬтжаЮЊецУќЬтЕФЪЧ__________.
Ђй![]() ВЛДцдкМЋжЕЃЛЂкШє
ВЛДцдкМЋжЕЃЛЂкШє![]() ЕФЗДКЏЪ§ЮЊ
ЕФЗДКЏЪ§ЮЊ![]() ЃЌЧвКЏЪ§
ЃЌЧвКЏЪ§![]() гыКЏЪ§
гыКЏЪ§![]() гаСНИіЙЋЙВЕуЃЌдђ
гаСНИіЙЋЙВЕуЃЌдђ![]() ЃЛЂлШє
ЃЛЂлШє![]() дк
дк![]() ЩЯЪЧМѕКЏЪ§ЃЌдђЪЕЪ§
ЩЯЪЧМѕКЏЪ§ЃЌдђЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЪЧ
ЕФШЁжЕЗЖЮЇЪЧ![]() ЃЛЂмШє
ЃЛЂмШє![]() ЃЌдђдк
ЃЌдђдк![]() ЕФЧњЯпЩЯДцдкСНЕуЃЌЪЙЕУЙ§етСНЕуЕФЧаЯпЛЅЯрДЙжБЃЎ
ЕФЧњЯпЩЯДцдкСНЕуЃЌЪЙЕУЙ§етСНЕуЕФЧаЯпЛЅЯрДЙжБЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЕу
жаЃЌЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() ЃЌЩшдВ
ЃЌЩшдВ![]() ЕФАыОЖЮЊ1ЃЌ дВаФдк
ЕФАыОЖЮЊ1ЃЌ дВаФдк![]() ЩЯ.
ЩЯ.

ЃЈ1ЃЉШєдВаФ![]() вВдкжБЯп
вВдкжБЯп![]() ЩЯЃЌЙ§Еу
ЩЯЃЌЙ§Еу![]() зїдВ
зїдВ![]() ЕФЧаЯпЃЌЧѓЧаЯпЗНГЬЃЛ
ЕФЧаЯпЃЌЧѓЧаЯпЗНГЬЃЛ
ЃЈ2ЃЉШєдВ![]() ЩЯДцдкЕу
ЩЯДцдкЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌЧѓдВаФ
ЃЌЧѓдВаФ![]() ЕФКсзјБъ
ЕФКсзјБъ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ОЙ§ЕуMЃЈЉ2ЃЌЉ1ЃЉЃЌРыаФТЪЮЊ
ОЙ§ЕуMЃЈЉ2ЃЌЉ1ЃЉЃЌРыаФТЪЮЊ![]() ЃЎЙ§ЕуMзїЧуаБНЧЛЅВЙЕФСНЬѕжБЯпЗжБ№гыЭждВCНЛгквьгкMЕФСэЭтСНЕуPЁЂQЃЎ
ЃЎЙ§ЕуMзїЧуаБНЧЛЅВЙЕФСНЬѕжБЯпЗжБ№гыЭждВCНЛгквьгкMЕФСэЭтСНЕуPЁЂQЃЎ
(Ђё)ЧѓЭждВCЕФЗНГЬЃЛ
ЃЈЂђЃЉЪдХаЖЯжБЯпPQЕФаБТЪЪЧЗёЮЊЖЈжЕЃЌжЄУїФуЕФНсТлЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊМзввСНСОГЕШЅЭЌвЛЛѕГЁзАЛѕЮяЃЌЛѕГЁУПДЮжЛФмИјвЛСОГЕзАЛѕЮяЃЌЫљвдШєСНСОГЕЭЌЪБЕНДяЃЌдђашвЊгавЛГЕЕШД§.вбжЊМзЁЂввСНГЕзАЛѕЮяашвЊЕФЪБМфЖМЮЊ20ЗжжгЃЌЬШШєМзЁЂввСНГЕЖМдкФГ1аЁЪБФкЕНДяИУЛѕГЁЃЌдђжСЩйгавЛСОГЕашвЊЕШД§зАЛѕЮяЕФИХТЪЪЧЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁЖжаЛЊШЫУёЙВКЭЙњЕРТЗНЛЭЈАВШЋЗЈЁЗЕк47ЬѕЕФЯрЙиЙцЖЈЃКЛњЖЏГЕааОШЫааКсЕРЪБЃЌгІЕБМѕЫйТ§ааЃЛгіааШЫе§дкЭЈЙ§ШЫааКсЕРЃЌгІЕБЭЃГЕШУааЃЌЫзГЦЁАРёШУАпТэЯпЁБЃЌЁЖжаЛЊШЫУёЙВКЭЙњЕРТЗНЛЭЈАВШЋЗЈЁЗ Ек90ЬѕЙцЖЈЃКЖдВЛРёШУааШЫЕФМнЪЛдБДІвдПл3ЗжЃЌЗЃПю50дЊЕФДІЗЃ.ЯТБэЪЧФГЪавЛжїИЩТЗПкМрПиЩшБИЫљзЅХФЕФ5ИідТФкМнЪЛдБВЛЁАРёШУАпТэЯпЁБааЮЊЭГМЦЪ§ОнЃК
дТЗн | 1 | 2 | 3 | 4 | 5 |
ЮЅеТМнЪЛдБШЫЪ§ | 120 | 105 | 100 | 90 | 85 |
ЃЈ1ЃЉЧыРћгУЫљИјЪ§ОнЧѓЮЅеТШЫЪ§![]() гыдТЗнжЎМфЕФЛиЙщжБЯпЗНГЬ
гыдТЗнжЎМфЕФЛиЙщжБЯпЗНГЬ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉНЛОЏДгет5ИідТФкЭЈЙ§ИУТЗПкЕФМнЪЛдБжаЫцЛњГщВщСЫ50ШЫЃЌЕїВщМнЪЛдБВЛЁАРёШУАпТэЯпЁБааЮЊгыМнСфЕФЙиЯЕЃЌЕУЕНШчЯТ![]() СаСЊБэЃКФмЗёОнДЫХаЖЯга
СаСЊБэЃКФмЗёОнДЫХаЖЯга![]() ЕФАбЮеШЯЮЊЁАРёШУАпТэЯпЁБааЮЊгыМнСфгаЙиЃП
ЕФАбЮеШЯЮЊЁАРёШУАпТэЯпЁБааЮЊгыМнСфгаЙиЃП
ВЛРёШУАпТэЯп | РёШУАпТэЯп | КЯМЦ | |
МнСфВЛГЌЙ§1Фъ | 22 | 8 | 30 |
МнСф1ФъвдЩЯ | 8 | 12 | 20 |
КЯМЦ | 30 | 20 | 50 |
ВЮПМЙЋЪНМАЪ§ОнЃК
 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЃЈЦфжа
ЃЈЦфжа![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаОйааЁАжабЇЩњЪЋДЪДѓШќЁБЃЌЗжГѕШќКЭИДШќСНИіНзЖЮНјааЃЌЙцЖЈЃКГѕШќГЩМЈДѓгк90ЗжЕФОпгаИДШќзЪИёЃЎФГаЃга800 УћбЇЩњВЮМгСЫГѕШќЃЌЫљгабЇЩњЕФГЩМЈОљдкЧјМф![]() ФкЃЌЦфЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪОЃЎ
ФкЃЌЦфЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪОЃЎ
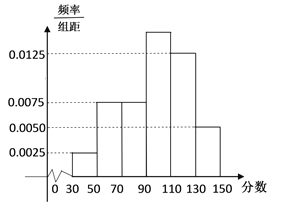
ЃЈЂёЃЉЧѓГѕШќЗжЪ§дкЧјМф![]() ФкЕФЦЕТЪЃЛ
ФкЕФЦЕТЪЃЛ
ЃЈЂђЃЉЧѓЛёЕУИДШќзЪИёЕФШЫЪ§ЃЛ
ЃЈЂѓЃЉОнДЫжБЗНЭМЙРЫубЇЩњГѕШќГЩМЈЕФЦНОљЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com