
【题目】已知函数![]() 。
。
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(2)若函数![]() 在
在![]() 处有极小值,求实数
处有极小值,求实数![]() 的值。
的值。
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:
(1)当![]() 时可得
时可得![]() ,进而可得函数在区间
,进而可得函数在区间![]() 上的单调性,求得函数的极大值和端点值后比较可得函数的最大值。(2)根据
上的单调性,求得函数的极大值和端点值后比较可得函数的最大值。(2)根据![]() 可得
可得![]() 或
或![]() ,然后分别代入解析式验证函数
,然后分别代入解析式验证函数![]() 是否在
是否在![]() 处有极小值,最后可得结论。
处有极小值,最后可得结论。
试题解析:
(1)当![]() 时,
时, ![]() ,
,
所以![]() ,
,
令![]() ,解得
,解得![]() 或
或![]() 。
。
当![]() 变化时,
变化时, ![]() 、
、![]() 的变化情况如下表:
的变化情况如下表:
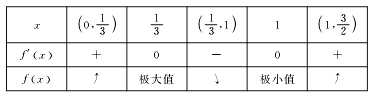
由表知当![]() 时,
时, ![]() 有极大值,且极大值为
有极大值,且极大值为![]() ;
;
又![]() ,
,
所以![]() 。
。
即函数![]() 在
在![]() 上的最大值为
上的最大值为![]() 。
。
(2)因为![]() ,
,
所以![]() ,
,
因为![]() 在
在![]() 处有极小值,
处有极小值,
所以![]() ,即
,即![]() ,
,
解得![]() 或
或![]() ,
,
①当![]() 时,
时, ![]() ,
,
故当![]() 时,
时, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() 单调递减;
单调递减;
![]() 时,
时, ![]() 单调递增。
单调递增。
所以函数![]() 在
在![]() 处有极小值,符合题意,
处有极小值,符合题意,
故![]() ,
,
②当![]() 时,
时, ![]() ,
,
故当![]() 时,
时, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() 单调递减;
单调递减;
![]() 时,
时, ![]() 单调递增,
单调递增,
所以函数![]() 在
在![]() 处有极大值,不符合题意,
处有极大值,不符合题意,
故![]() 不成立,舍去。
不成立,舍去。
综上![]() 。
。


科目:高中数学 来源: 题型:
【题目】已知直线l:y=﹣x+1与椭圆C: ![]() =1(a>b>0))相交于不同的两点A、B,且线段AB的中点P的坐标为(
=1(a>b>0))相交于不同的两点A、B,且线段AB的中点P的坐标为( ![]() ,
, ![]() )
) 
(1)求椭圆C离心率;
(2)设O为坐标原点,且2|OP|=|AB|,求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由 ![]() 算得,
算得, ![]() .
.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两地相距![]() ,货车从甲地匀速行驶到乙地,速度不得超过
,货车从甲地匀速行驶到乙地,速度不得超过![]() ,已知货车每小时的运输成本(单位:圆)由可变本和固定组成组成,可变成本是速度平方的
,已知货车每小时的运输成本(单位:圆)由可变本和固定组成组成,可变成本是速度平方的![]() 倍,固定成本为
倍,固定成本为![]() 元.
元.
(1)将全程匀速匀速成本![]() (元)表示为速度
(元)表示为速度![]() 的函数,并指出这个函数的定义域;
的函数,并指出这个函数的定义域;
(2)若![]() ,为了使全程运输成本最小,货车应以多大的速度行驶?
,为了使全程运输成本最小,货车应以多大的速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() +y2=1,A,B,C,D为椭圆上四个动点,且AC,BD相交于原点O,设A(x1 , y1),B(x2 , y2)满足
+y2=1,A,B,C,D为椭圆上四个动点,且AC,BD相交于原点O,设A(x1 , y1),B(x2 , y2)满足 ![]() =
= ![]() .
.
(1)求证: ![]() +
+ ![]() =
= ![]() ;
;
(2)kAB+kBC的值是否为定值,若是,请求出此定值,并求出四边形ABCD面积的最大值,否则,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法中错误的是
A. 在频率分布直方图中,中位数左边和右边的直方图的面积相等 .
B. 一个样本的方差是![]() ,则这组数据的总和等于60.
,则这组数据的总和等于60.
C. 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越差.
D. 对于命题![]() 使得
使得![]() <0,则
<0,则![]() ,使
,使![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们为了探究函数![]() 的部分性质,先列表如下:
的部分性质,先列表如下:
| … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.004 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
观察表中![]() 值随
值随![]() 值变化的特点,完成以下的问题.
值变化的特点,完成以下的问题.
首先比较容易看得出来:此函数在区间![]() 上是递减的;
上是递减的;
(1)函数![]() 在区间 上递增
在区间 上递增
当![]() 时,
时,![]() = .
= .
(2)请你根据上面性质作出此函数的大概图像;
(3)试用函数单调性的定义证明:函数![]() 在区间
在区间![]() 上为减函数.
上为减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义域为R的偶函数,当![]() 时,f(x)=x2-2x
时,f(x)=x2-2x

(1)求出函数f(x)在R上的解析式;
(2)画出函数f(x)的图象,并根据图象写出f(x)的单调区间.
(3)求使f(x)=1时的x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com