
【题目】已知函数![]() (
(![]() ,
, ![]() ),曲线
),曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() ,
, ![]() 的值;
的值;
(Ⅱ)证明: ![]() ;
;
(Ⅲ)已知满足![]() 的常数为
的常数为![]() .令函数
.令函数![]() (其中
(其中![]() 是自然对数的底数,
是自然对数的底数, ![]() ),若
),若![]() 是
是![]() 的极值点,且
的极值点,且![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
, ![]() .(2)详见解析;(3)
.(2)详见解析;(3)![]()
【解析】试题分析:
(1)由导函数与切线方程的关系可得![]() ,
, ![]() .
.
(2)利用题意构造新函数![]()
![]() ,结合新函数的性质即可证得
,结合新函数的性质即可证得 ![]() ;
;
(3)由题意![]() ,
,
当![]() 时,
时, ![]() 无极值,不符合题意;
无极值,不符合题意;
当![]() 时,
时, ![]() 是函数
是函数![]() 的唯一极值点,也是它的唯一最大值点,可得
的唯一极值点,也是它的唯一最大值点,可得![]()
![]()
![]() .
.
由题意考察函数![]() ,可得
,可得![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(Ⅰ)![]() 的导函数
的导函数![]() ,
,
由曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,知
,知![]() ,
, ![]() ,
,
所以![]() ,
, ![]() .
.
(Ⅱ)令![]()
![]() ,则
,则![]()
![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增,
所以,当![]() 时,
时, ![]() 取得极小值,也即最小值,该最小值为
取得极小值,也即最小值,该最小值为![]() ,
,
所以![]() ,即不等式
,即不等式![]() 成立.
成立.
(Ⅲ)函数![]() (
(![]() ),则
),则![]() ,
,
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 内单调递增,
内单调递增, ![]() 无极值,不符合题意;
无极值,不符合题意;
当![]() 时,由
时,由![]() ,得
,得![]() ,
,
结合![]() ,
, ![]() 在
在![]() 上的图象可知,关于
上的图象可知,关于![]() 的方程
的方程![]() 一定有解,其解为
一定有解,其解为![]() (
(![]() ),且当
),且当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 内单调递增;当
内单调递增;当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 内单调递减.
内单调递减.
则![]() 是函数
是函数![]() 的唯一极值点,也是它的唯一最大值点,
的唯一极值点,也是它的唯一最大值点,
![]() 也是
也是![]() 在
在![]() 上的唯一零点,即
上的唯一零点,即![]() ,则
,则![]() .
.
所以![]()
![]()
![]() .
.
由于![]() 恒成立,则
恒成立,则![]() ,即
,即![]() ,(*)
,(*)
考察函数![]() ,则
,则![]() ,
,
所以![]() 为
为![]() 内的增函数,且
内的增函数,且![]() ,
, ![]() ,
,
又常数![]() 满足
满足![]() ,即
,即![]() ,
,
所以, ![]() 是方程
是方程![]() 的唯一根,
的唯一根,
于是不等式(*)的解为![]() ,
,
又函数![]() (
(![]() )为增函数,故
)为增函数,故![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某理财公司有两种理财产品![]() 和
和![]() .这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
.这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品![]()
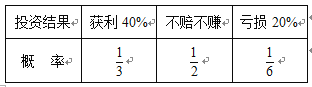
产品![]() (其中
(其中![]() )
)
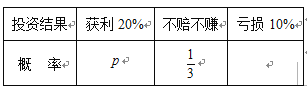
(Ⅰ)已知甲、乙两人分别选择了产品![]() 和产品
和产品![]() 进行投资,如果一年后他们中至少有一人获利的概率大于
进行投资,如果一年后他们中至少有一人获利的概率大于![]() ,求
,求![]() 的取值范围;
的取值范围;
(Ⅱ)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品![]() 和产品
和产品![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S. ①当 ![]() 时,S为四边形
时,S为四边形
②截面在底面上投影面积恒为定值 ![]()
③不存在某个位置,使得截面S与平面A1BD垂直
④当 ![]() 时,S与C1D1的交点满足C1R1=
时,S与C1D1的交点满足C1R1= ![]()
其中正确命题的个数为 ( )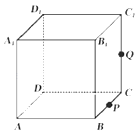
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() +y2=1的左右焦点分别为F1 , F2 , 直线l过椭圆的右焦点F2与椭圆交于A,B 两点, (Ⅰ)当直线l的斜率为1,点P为椭圆上的动点,满足使得△ABP的面积为
+y2=1的左右焦点分别为F1 , F2 , 直线l过椭圆的右焦点F2与椭圆交于A,B 两点, (Ⅰ)当直线l的斜率为1,点P为椭圆上的动点,满足使得△ABP的面积为 ![]() 的点P有几个?并说明理由.
的点P有几个?并说明理由.
(Ⅱ)△ABF1的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时直线l的方程,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的二次方程x2+2mx+2m+1=0.
(1)若方程有两个正根,求m的取值范围.
(2)若方程有两根,其中一根在区间(﹣1,0)内,另一根在区间(1,3)内,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 支篮球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是
支篮球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是![]() .单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:
.单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:
![]() :恰有四支球队并列第一名为不可能事件;
:恰有四支球队并列第一名为不可能事件; ![]() :有可能出现恰有两支球队并列第一名;
:有可能出现恰有两支球队并列第一名;
![]() :每支球队都既有胜又有败的概率为
:每支球队都既有胜又有败的概率为![]() ;
; ![]() :五支球队成绩并列第一名的概率为
:五支球队成绩并列第一名的概率为![]() .
.
其中真命题是
A. ![]() ,
,![]() ,
,![]() B.
B. ![]() ,
,![]() ,
,![]() C.
C. ![]() .
.![]() .
.![]() D.
D. ![]() .
.![]() .
.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com