
【题目】求函数f(x)=sinx+cosx+sinxcosx的值域________.
【答案】[﹣1, ![]() +
+ ![]() ]
]
【解析】解:令t=sinx+cosx= ![]() sin(x+
sin(x+ ![]() ),
),
则﹣ ![]() ≤t≤
≤t≤ ![]() ,t2=1+2sinxcosx,
,t2=1+2sinxcosx,
则sinxcosx= ![]() ,
,
则f(x)=sinx+cosx+sinxcosx
=t+ ![]() =
= ![]() (t2+2t﹣1)
(t2+2t﹣1)
= ![]() (t+1)2﹣1;
(t+1)2﹣1;
∵﹣ ![]() ≤t≤
≤t≤ ![]() ,
,
∴﹣1≤ ![]() (t+1)2﹣1≤
(t+1)2﹣1≤ ![]() +
+ ![]() ;
;
故函数f(x)=sinx+cosx+sinxcosx的值域为[﹣1, ![]() +
+ ![]() ].
].
【考点精析】掌握函数的值域和三角函数的最值是解答本题的根本,需要知道求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的;函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
【题目】(本小题满分14分)如图,四棱锥![]() 的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,
的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,连结
的中点,连结![]() .求证:
.求证:
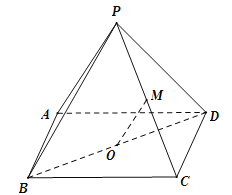
(1)![]() ∥平面
∥平面![]() ;
;
(2)![]() ⊥平面
⊥平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10000m,速度为180km(千米)/h(小时),飞机先看到山顶的俯角为15°,经过420s(秒)后又看到山顶的俯角为45°,求山顶的海拔高度(取 ![]() ,
, ![]() ).
). 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 ![]() =(1,2)
=(1,2)
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标;
的坐标;
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 与
与 ![]() 的夹角θ.
的夹角θ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个水轮的半径为4m,水轮圆心O距离水面2m,已知水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点p0)开始计算时间. 
(1)将点p距离水面的高度z(m)表示为时间t(s)的函数;
(2)点p第一次到达最高点大约需要多少时间?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,D为AB的中点.
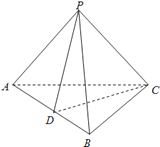
(1)与BC平行的平面PDE交AC于点E,判断点E在AC上的位置并说明理由如下:
(2)若PA=PB,且△PCD为锐角三角形,又平面PCD⊥平面ABC,求证:AB⊥PC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,当∠xOy=α,且α∈(0, ![]() )∪(
)∪( ![]() ,π)时,定义平面坐标系xOy为α﹣仿射坐标系.在α﹣仿射坐标系中,任意一点P的斜坐标这样定义:
,π)时,定义平面坐标系xOy为α﹣仿射坐标系.在α﹣仿射坐标系中,任意一点P的斜坐标这样定义: ![]() 、
、 ![]() 分别为与x轴、y轴正向相同的单位向量,若
分别为与x轴、y轴正向相同的单位向量,若 ![]() =x
=x ![]() +y
+y ![]() ,则记为
,则记为 ![]() =(x,y).现给出以下说法:
=(x,y).现给出以下说法:
①在α﹣仿射坐标系中,已知 ![]() =(1,2),
=(1,2), ![]() =(3,t),若
=(3,t),若 ![]() ∥
∥ ![]() ,则t=6;
,则t=6;
②在α﹣仿射坐标系中,若 ![]() =(
=( ![]() ,
, ![]() ),若
),若 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ),则
),则 ![]()
![]() =0;
=0;
③在60°﹣仿射坐标系中,若P(2,﹣1),则| ![]() |=
|= ![]() ;
;
其中说法正确的有 . (填出所有说法正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P-ABC中,D为AB的中点。

(1)与BC平行的平面PDE交AC于点E,判断点E在AC上的位置并说明理由如下:
(2)若PA=PB,且△PCD为锐角三角形,又平面PCD⊥平面ABC,求证:AB⊥PC。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知PA垂直于矩形ABCD所在的平面,M,N分别是AB,PC的中点,若∠PDA=45°, 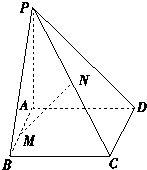
(1)求证:MN∥平面PAD且MN⊥平面PCD.
(2)探究矩形ABCD满足什么条件时,有PC⊥BD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com