
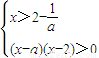 ,下面对a进行分类讨论:当1<a<2时,当a=2时,当a>2,从而通过解不等式组求得使得p、q都成立的x的集合.
,下面对a进行分类讨论:当1<a<2时,当a=2时,当a>2,从而通过解不等式组求得使得p、q都成立的x的集合.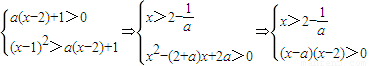 ---(4分)
---(4分)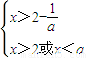 ,而
,而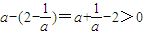 ,
,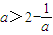 ,
,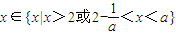 ;----(6分)
;----(6分)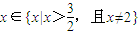 ;----(8分)
;----(8分)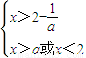 ,----(10分)
,----(10分)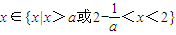 .----(12分).
.----(12分).

科目:高中数学 来源:2012-2013学年新课标高三(上)数学一轮复习单元验收1(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com