
【题目】求下列各式极限:
(1)![]() ;
;
(2)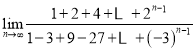 ;
;
(3)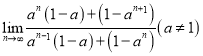 ;
;
(4)![]() ;
;
(5)![]() ;
;
(6)![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析;(4)
;(3)见解析;(4)![]() ;(5)见解析;(6)
;(5)见解析;(6)![]() .
.
【解析】
(1)在分式的分子和分母中同时除以![]() ,再利用常见数列的极限可求得所求极限的值;
,再利用常见数列的极限可求得所求极限的值;
(2)利用等比数列求和公式化简分式的分子和分母,然后在分式的分子和分母中同时除以![]() ,再利用常见数列的极限可求得所求极限的值;
,再利用常见数列的极限可求得所求极限的值;
(3)化简所求极限为![]() ,然后分
,然后分![]() 、
、![]() 、
、![]() 三种情况讨论,利用常用数列的极限可求得所求极限的值;
三种情况讨论,利用常用数列的极限可求得所求极限的值;
(4)在分式的分子和分母中同时除以![]() ,再利用常见数列的极限可求得所求极限的值;
,再利用常见数列的极限可求得所求极限的值;
(5)在所求的分式的分子和分母中同时除以![]() ,然后分
,然后分![]() 、
、![]() 、
、![]() 三种情况讨论,利用常见数列的极限可求得所求极限的值;
三种情况讨论,利用常见数列的极限可求得所求极限的值;
(6)利用等比数列求和公式化简分母,然后在分式的分子和分母中同时除以![]() ,利用常见数列的极限可求得所求极限的值.
,利用常见数列的极限可求得所求极限的值.
(1)原式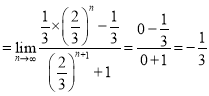 ;
;
(2)![]() ,
,![]() ,
,
![]() 原式
原式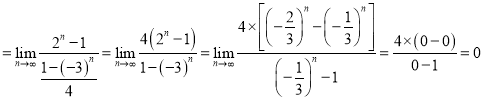 ;
;
(3)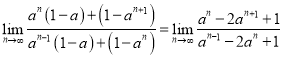 .
.
当![]() 时,原极限不存在;
时,原极限不存在;
当![]() 时,原式
时,原式![]() ;
;
当![]() 时,原式
时,原式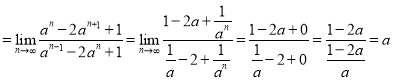 .
.
综上所述,当![]() 时,原极限不存在;当
时,原极限不存在;当![]() 时,原式
时,原式![]() ;当
;当![]() 时,原式
时,原式![]() ;
;
(4)![]() ,原式
,原式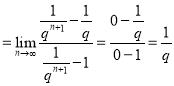 ;
;
(5)![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,原式
,原式![]() ;
;
当![]() 时,
时,![]() ,原式
,原式![]() ;
;
当![]() 时,
时,![]() ,原式
,原式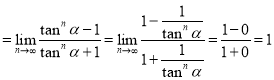 .
.
综上所述,当![]() 时,原式
时,原式![]() ;当
;当![]() 时,原式
时,原式![]() ;当
;当![]() 时,原式
时,原式![]() ;
;
(6)![]() ,
,![]() ,则
,则![]() ,
,
所以,原式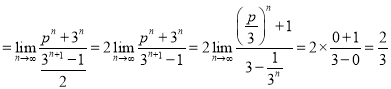 .
.


科目:高中数学 来源: 题型:
【题目】
按照某学者的理论,假设一个人生产某产品单件成本为![]() 元,如果他卖出该产品的单价为
元,如果他卖出该产品的单价为![]() 元,则他的满意度为
元,则他的满意度为![]() ;如果他买进该产品的单价为
;如果他买进该产品的单价为![]() 元,则他的满意度为
元,则他的满意度为![]() .如果一个人对两种交易(卖出或买进)的满意度分别为
.如果一个人对两种交易(卖出或买进)的满意度分别为![]() 和
和![]() ,则他对这两种交易的综合满意度为
,则他对这两种交易的综合满意度为![]() .
.
现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为![]() 元和
元和![]() 元,甲买进A与卖出B的综合满意度为
元,甲买进A与卖出B的综合满意度为![]() ,乙卖出A与买进B的综合满意度为
,乙卖出A与买进B的综合满意度为![]()
(1)求![]() 和
和![]() 关于
关于![]() 、
、![]() 的表达式;当
的表达式;当![]() 时,求证:
时,求证:![]() =
=![]() ;
;
(2)设![]() ,当
,当![]() 、
、![]() 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为
分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为![]() ,试问能否适当选取
,试问能否适当选取![]() 、
、![]() 的值,使得
的值,使得![]() 和
和![]() 同时成立,但等号不同时成立?试说明理由。
同时成立,但等号不同时成立?试说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣sinx,记f(x)的导函数为f'(x).
(1)若h(x)=ax![]() f'(x)是(0,+∞)上的单调递增函数,求实数a的取值范围;
f'(x)是(0,+∞)上的单调递增函数,求实数a的取值范围;
(2)若x∈(0,2π),试判断函数f(x)的极值点个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是某高架桥箱梁的横截面,它由上部路面和下部支撑箱两部分组成.如图2,路面宽度![]() ,下部支撑箱CDEF为等腰梯形(
,下部支撑箱CDEF为等腰梯形(![]() ),且
),且![]() .为了保证承重能力与稳定性,需下部支撑箱的面积为
.为了保证承重能力与稳定性,需下部支撑箱的面积为![]() ,高度为2m且
,高度为2m且![]() ,若路面AB.侧边CF和DE,底部EF的造价分别为4a千元/m,5a千元/m,6a千元/m(a为正常数),
,若路面AB.侧边CF和DE,底部EF的造价分别为4a千元/m,5a千元/m,6a千元/m(a为正常数),![]() .
.

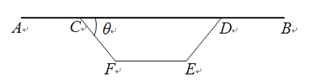
(1)试用θ表示箱梁的总造价y(千元);
(2)试确定cosθ的值,使总造价最低?并求最低总造价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C是椭圆W:![]() 上的三个点,O是坐标原点.
上的三个点,O是坐标原点.
(I)当点B是W的右顶点,且四边形OABC为菱形时,求此菱形的面积.
(II)当点B不是W的顶点时,判断四边形OABC是否可能为菱形,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度.某地区在2015 年以前的年均脱贫率(脱离贫困的户数占当年贫困户总数的比)为![]() .2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
.2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
实施项目 | 种植业 | 养殖业 | 工厂就业 | 服务业 |
参加用户比 |
|
|
|
|
脱贫率 |
|
|
|
|
那么![]() 年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )
年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校组织的一次篮球定点投篮比赛中,两人一对一比赛规则如下:若某人某次投篮命中,则由他继续投篮,否则由对方接替投篮. 现由甲、乙两人进行一对一投篮比赛,甲和乙每次投篮命中的概率分别是![]() ,
,![]() .两人共投篮3次,且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.则3次投篮的人依次是甲、甲、乙的概率___________;
.两人共投篮3次,且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.则3次投篮的人依次是甲、甲、乙的概率___________;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,二面角α﹣1﹣β的平面角的大小为60°,A,B是1上的两个定点,且AB=2.C∈α,D∈β,满足AB与平面BCD所成的角为30°,且点A在平面BCD上的射影H在△BCD的内部(包括边界),则点H的轨迹的长度等于( )
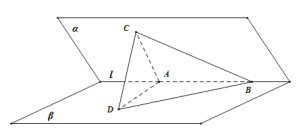
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com