
【题目】设离心率为 ![]() 的椭圆
的椭圆![]() 的左、右焦点为
的左、右焦点为![]() , 点P是E上一点,
, 点P是E上一点, ![]() ,
, ![]() 内切圆的半径为
内切圆的半径为 ![]() .
.
(1)求E的方程;
(2)矩形ABCD的两顶点C、D在直线![]() 上,A、B在椭圆E上,若矩形ABCD的周长为
上,A、B在椭圆E上,若矩形ABCD的周长为 ![]() , 求直线AB的方程.
, 求直线AB的方程.
科目:高中数学 来源: 题型:
【题目】△ABC的三个内角A,B,C对应的边分别a,b,c,且acosC,bcosB,ccosA成等差数列,则角B等于( )
A.30°
B.60°
C.90°
D.120°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在[﹣1,1]上的奇函数,当x∈[﹣1,0]时,函数解析式为 ![]() .
.
(Ⅰ)求f(x)在[0,1]上的解析式;
(Ⅱ)求f(x)在[0,1]上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在(0,+∞)上的函数f(x)满足下面三个条件:
①对任意正数a,b,都有f(a)+f(b)=f(ab);
②当x>1时,f(x)<0;
③f(2)=﹣1
(I)求f(1)和 ![]() 的值;
的值;
(II)试用单调性定义证明:函数f(x)在(0,+∞)上是减函数;
(III)求满足f(log4x)>2的x的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,甲、乙两位同学要测量河对岸A,B两点间的距离,今沿河岸选取相距40米的C,D两点,测得∠ACB=60°,∠BCD=45°,∠ADC=30°,∠CDB=90°求A,B两点间的距离. 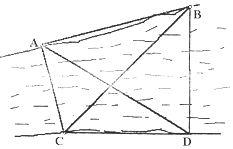
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)为定义在R上的奇函数,且在(0,+∞)内是增函数,又f(2)=0,则不等式x5f(x)>0的解集为( )
A.(﹣2,0)∪(2,+∞)
B.(﹣∞,﹣2)∪(0,2)
C.(﹣2,0)∪(0,2)
D.(﹣∞,﹣2)∪(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x+1),g(x)=loga(1﹣x)(a>0且a≠1).
(1)求f(x)+g(x)的定义域;
(2)判断函数f(x)+g(x)的奇偶性,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)已知直线l经过点P(4,1),且在两坐标轴上的截距相等,求直线l的方程;
(2)已知直线l经过点P(3,4),且直线l的倾斜角为θ(θ≠90°),若直线l经过另外一点(cosθ,sinθ),求此时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com