
【题目】已知在圆x2+y2﹣4x+2y=0内,过点E(1,0)的最长弦和最短弦分别是AC和BD,则四边形ABCD的面积为( )
A.![]()
B.6 ![]()
C.![]()
D.2 ![]()
科目:高中数学 来源: 题型:
【题目】国际奥委会于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地,目前德国汉堡,美国波士顿等申办城市因市民担心赛事费用超支而相继退出,某机构为调查我国公民对申办奥运会的态度,选了100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | _______ | _______ | 80 |
年龄大于50岁 | 10 | _______ | _______ |
合计 | _______ | 70 | 100 |
(1)根据已知数据,把表格填写完整;
(2)是否有95%的把握认为年龄与支持申办奥运有关?
附表:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.814 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)= ![]() +lnx在[1,+∞)上为增函数,且θ∈(0,π),f(x)=mx﹣
+lnx在[1,+∞)上为增函数,且θ∈(0,π),f(x)=mx﹣ ![]() ﹣lnx(m∈R). (Ⅰ)求θ的值;
﹣lnx(m∈R). (Ⅰ)求θ的值;
(Ⅱ)若f(x)﹣g(x)在[1,+∞)上为单调函数,求m的取值范围;
(Ⅲ)设h(x)= ![]() ,若在[1,e]上至少存在一个x0 , 使得f(x0)﹣g(x0)>h(x0)成立,求m的取值范围.
,若在[1,e]上至少存在一个x0 , 使得f(x0)﹣g(x0)>h(x0)成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察下列方程,并回答问题:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;…
;…
(1)请你根据这列方程的特点写出第![]() 个方程;
个方程;
(2)直接写出第2009个方程的根;
(3)说出这列方程的根的一个共同特点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地空气中出现污染,须喷洒一定量的去污剂进行处理.据测算,每喷洒1个单位的去污剂,空气中释放的浓度y(单位:毫克/立方米)随着时间x(单位:天)变化的函数关系式近似为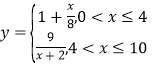 ,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和.由实验知,当空气中去污剂的浓度不低于4(毫克/立方米)时,它才能起到去污作用.
,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和.由实验知,当空气中去污剂的浓度不低于4(毫克/立方米)时,它才能起到去污作用.
(Ⅰ)若一次喷洒4个单位的去污剂,则去污时间可达几天?
(Ⅱ)若第一次喷洒2个单位的去污剂,6天后再喷洒![]()
![]() 个单位的去污剂,要使接下来的4天中能够持续有效去污,试求
个单位的去污剂,要使接下来的4天中能够持续有效去污,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项等比数列{an}前n项和为Sn , 且满足S3= ![]() ,a6 , 3a5 , a7成等差数列. (Ⅰ)求数列{an}的通项公式;
,a6 , 3a5 , a7成等差数列. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列bn= ![]() ,且数列bn的前n项的和Tn , 试比较Tn与
,且数列bn的前n项的和Tn , 试比较Tn与 ![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P为⊙O外一点,PC交⊙O于F,C,PA切⊙O于A,B为线段PA的中点,BC交⊙O于D,线段PD的延长线与⊙O交于E,连接FE.求证:
(Ⅰ)△PBD∽△CBP;
(Ⅱ)AP∥FE.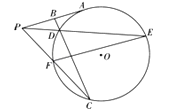
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com