
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)试讨论函数![]() 的单调性;
的单调性;
(2)若![]() ,试证明:
,试证明:![]() .
.
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点为原点,其焦点
的顶点为原点,其焦点![]() 到直线
到直线![]() 的距离为
的距离为![]() .设
.设![]() 为直线
为直线![]() 上的点,过点
上的点,过点![]() 作抛物线
作抛物线![]() 的两条切线
的两条切线![]() ,其中
,其中![]() 为切点.
为切点.
(1) 求抛物线![]() 的方程;
的方程;
(2) 当点![]() 为直线
为直线![]() 上的定点时,求直线
上的定点时,求直线![]() 的方程;
的方程;
(3) 当点![]() 在直线
在直线![]() 上移动时,求
上移动时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】法国有个名人叫做布莱尔·帕斯卡,他认识两个赌徒,这两个赌徒向他提出一个问题,他们说,他们下赌金之后,约定谁先赢满5局,谁就获得全部赌金700法郎,赌了半天,甲赢了4局,乙赢了3局,时间很晚了,他们都不想再赌下去了.假设每局两赌徒输赢的概率各占![]() ,每局输赢相互独立,那么这700法郎如何分配比较合理( )
,每局输赢相互独立,那么这700法郎如何分配比较合理( )
A.甲400法郎,乙300法郎B.甲500法郎,乙200法郎
C.甲525法郎,乙175法郎D.甲350法郎,乙350法郎
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() ,
,![]() 是三个不同平面,
是三个不同平面,![]() ,
,![]() 是两条不同直线,有下列三个条件:(1)
是两条不同直线,有下列三个条件:(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() ,
,![]() .如果命题“
.如果命题“![]() ,
,![]() ,且__________,则
,且__________,则![]() ”为真命题,则可以在横线处填入的条件是__________(把所有正确的序号填上).
”为真命题,则可以在横线处填入的条件是__________(把所有正确的序号填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图甲,AD,BC是等腰梯形CDEF的两条高,![]() ,点M是线段AE的中点,将该等腰梯形沿着两条高AD,BC折叠成如图乙所示的四棱锥P-ABCD(E,F重合,记为点P).
,点M是线段AE的中点,将该等腰梯形沿着两条高AD,BC折叠成如图乙所示的四棱锥P-ABCD(E,F重合,记为点P).
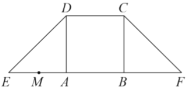
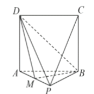
甲 乙
(1)求证:![]() ;
;
(2)求点M到平面BDP距离h.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据有关资料预测,某市下月1—14日的空气质量指数趋势如下图所示.,根据已知折线图,解答下面的问题:
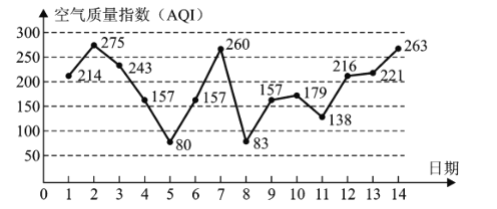
(1)求污染指数的众数及前五天污染指数的平均值;(保留整数)
(2)为了更好发挥空气质量监测服务人民的目的,监测部门在发布空气质量指数的同时,也给出了出行建议,比如空气污染指数大于150时需要戴口罩,超过200时建议减少外出活动等等.如果某人事先没有注意到空气质量预报,而在1—12号这12天中随机选定一天,欲在接下来的两天中(不含选定当天)进行外出活动.求其外出活动的两天期间.
①恰好都遭遇重度及以上污染天气的概率;
②至少有一天能避开重度及以上污染天气的概率.
附:空气质量等级参考表:
|
|
|
|
|
|
|
等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】哈三中团委组织了“古典诗词”的知识竞赛,从参加考试的学生中抽出60名学生(男女各30名),将其成绩分成六组![]() ,
,![]() ,…,
,…,![]() ,其部分频率分布直方图如图所示.
,其部分频率分布直方图如图所示.
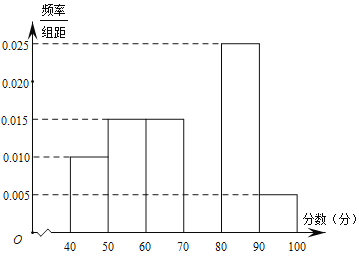
(Ⅰ)求成绩在![]() 的频率,补全这个频率分布直方图,并估计这次考试的众数和中位数;
的频率,补全这个频率分布直方图,并估计这次考试的众数和中位数;
(Ⅱ)从成绩在![]() 和
和![]() 的学生中选两人,求他们在同一分数段的概率;
的学生中选两人,求他们在同一分数段的概率;
(Ⅲ)我们规定学生成绩大于等于80分时为优秀,经统计男生优秀人数为4人,补全下面表格,并判断是否有99%的把握认为成绩是否优秀与性别有关?
优秀 | 非优秀 | 合计 | |
男 | 4 | 30 | |
女 | 30 | ||
合计 | 60 |
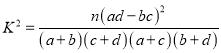
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com