Question

18．已知函数g（x）=ax²-2ax+1+b（a＞0）在区间[2，3]上有最大值4和最小值1，设f（x）=$\frac{g（x）}{x}$
（1）求a，b的值；
（2）若不等式f（2^x）-k•2^x≥0在x∈[-1，1]上有解，求实数k的取值范围；
（3）若f（2^x-1）+k$\frac{2^x}{{|{{2^x}-1}|}}$-3k=0有三个不同的实数根，求实数k的取值范围．

Answer 1

分析 （1）由函数g（x）=a（x-1）²+1+b-a，a＞0，所以g（x）在区间[2，3]上是增函数，得到方程组，由此解得a、b的值，
（2）不等式可化为 2^x+$\frac{1}{2x}$-2≥k•2^x，故有 k≤t²-2t+1，t∈[$\frac{1}{2}$，2]，求出h（t）=t²-2t+1的最大值，从而求得k的取值范围，
（3）方程f（|2^k-1|）+k•$\frac{2}{|2k-1|}$-3k=0⇒|2^x-1|²-（2+3k）|2^x-1|+（1+2k）=0，（|2^x-1|≠0），令|2^x-1|=t，则t²-（2+3k）t+（1+2k）=0（t≠0），构造函数h（t）=t²-（2+3k）t+（1+2k），通过数形结合与等价转化的思想即可求得k的范围．

解答 解：（1）函数g（x）=ax²-2ax+b+1=a（x-1）²+1+b-a，
因为a＞0，所以g（x）在区间[2，3]上是增函数，故 $\left\{\begin{array}{l}{g（2）=1}\\{g（3）=4}\end{array}\right.$，解得 $\left\{\begin{array}{l}{a=1}\\{b=0}\end{array}\right.$；
（2）由已知可得f（x）=x+$\frac{1}{x}$-2，所以，不等式f（2^x）-k•2^x≥0可化为 2^x+$\frac{1}{2x}$-2≥k•2^x，
可化为 1+（$\frac{1}{2x}$）²-2•$\frac{1}{2x}$≥k，令t=$\frac{1}{2x}$，则 k≤t²-2t+1．
因 x∈[-1，1]，故 t∈[$\frac{1}{2}$，2]．故k≤t²-2t+1在t∈[$\frac{1}{2}$，2]上能成立．
记h（t）=t²-2t+1，因为 t∈[$\frac{1}{2}$，2]，故 h（t）_max =h（2）=1，
所以k的取值范围是（-∞，1]；
（3）方程f（|2^k-1|）+k•$\frac{2}{|2k-1|}$-3k=0可化为：
|2^x-1|²-（2+3k）|2^x-1|+（1+2k）=0，|2^x-1|≠0，
令|2^x-1|=t，则方程化为
t²-（2+3k）t+（1+2k）=0（t≠0），
∵方程f（|2^k-1|）+k•$\frac{2}{|2k-1|}$-3k=0有三个不同的实数解，
∴由t=|2^x-1|的图象知，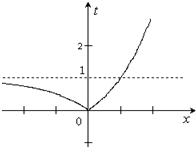

t²-（2+3k）t+（1+2k）=0（t≠0），有两个根t₁、t₂，
且0＜t₁＜1＜t₂或0＜t₁＜1，t₂=1．
记h（t）=t²-（2+3k）t+（1+2k），
则 $\left\{\begin{array}{l}{h（0）=1+2k＞0}\\{h（1）=-k＜0}\end{array}\right.$，或 $\left\{\begin{array}{l}{h（0）=1+2k＞0}\\{h（1）=-k=0}\\{0＜\frac{2+3k}{2}＜1}\end{array}\right.$，
∴k＞0．

点评 本题考查二次函数在闭区间上的最值，考查函数恒成立问题问题，考查数形结合与等价转化、函数与方程思想的综合应用，属于难题．