如图，甲船以每小时
海里的速度向正北方航行，乙船按固定方向匀速直线航行，当甲船位于
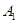处时，乙船位于甲船的北偏西
方向的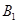
处，此时两船相距
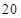海里，当甲船航行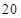分钟到达
处时，乙船航行到甲船的北偏西
方向的
处，此时两船相距
海里，问乙船每小时航行多少海里？
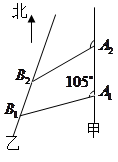
科目：高中数学 来源： 题型：解答题
如图，制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图形．由对称性，图中8个三角形都是全等的三角形，设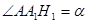
．
（1）试用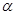
表示
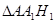的面积；
（2）求八角形所覆盖面积的最大值，并指出此时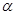的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
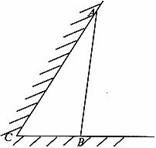
如图所示，某饲养场要建造一间两面靠墙的三角形露天养殖场，已知已有两面墙的夹角为60°（即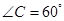
），现有可供建造第三面围墙的材料60米（两面墙的长均大于60米），为了使得小老虎能健康成长，要求所建造的三角形露天活动室尽可能大，记
，
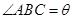(1)问当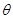
为多少时，所建造的三角形露天活动室的面积最大？
(2)若饲养场建造成扇形，养殖场的面积能比（1）中的最大面积更大？说明理由。
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
在△ABC中，
分别为角A、B、C的对边，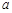
=3,△ABC的面积为6，
，D为△ABC内任一点，点D到三边距离之和为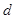
。
(1)求：角A的正弦值；
(2)求：边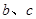
；
(3)求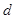：的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，依题意可知
，求得
的值，推断出
是等边三角形，进而求得
，在
中，利用余弦定理，可得
，从而可求出
的值，最终可求得乙船的速度．
，
，
，又
，
是等边三角形，
，由已知，
，
，在
中，由余弦定理，
．
．因此，乙船的速度的大小为
（海里/小时）．答：乙船每小时航行
中，角
，
，
所对的边分别是
，
，
，已知
，
.
，求
，求
中内角
的对边分别为
，已知
，
.
的值；（2）若
为
中点，且
的面积为
，求
的长度.
的图像变换得到
的图像；
中，角
所对的边分别是
，若
，求
的取值范围
中，角
，
，
对应的边分别是
，已知
.
的面积
，求
的值.
.
的值；
，
,求
的面积.