
分析 (1)根据二次函数的性质即可求出函数的最小值,
(2)先化为分段函数,再画图即可,并根据图象写出其单调减区间,
(3)由题意可知y=g(x)与y=log2m的两图象至少有三个交点,结合图象可得.
解答 解:(1)∵f(x)在[-1,1]上是增函数,在(1,2]上是减函数,
∴f(x)min=f(-1)=-1-2=-3.
(2)∵$g(x)=\left\{\begin{array}{l}-{x^2}+2x,0≤x≤2\\{x^2}-2x,x<0或x>2\end{array}\right.$
∴作出函数g(x)的图象如图,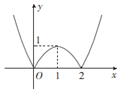
故函数g(x)的单调递减区间是(-∞,0)和(1,2).
(3)由题意可知y=g(x)与y=log2m的两图象至少有三个交点,
所以根据(2)中图象可得0<log2m≤1,
∴1<m≤2,
即m∈(1,2].
点评 本题考查了二次函数的图象和性质以及绝对值函数图象的画法和参数的取值范围,属于中档题


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:高中数学 来源: 题型:解答题
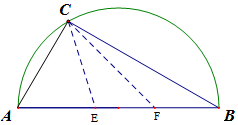 如图,有一直径为8米的半圆形空地,现计划种植果树,但需要有辅助光照.半圆周上的C处恰有一可旋转光源满足果树生长的需要,该光源照射范围是$∠ECF=\frac{π}{6}$,点E,F在直径AB上,且$∠ABC=\frac{π}{6}$.
如图,有一直径为8米的半圆形空地,现计划种植果树,但需要有辅助光照.半圆周上的C处恰有一可旋转光源满足果树生长的需要,该光源照射范围是$∠ECF=\frac{π}{6}$,点E,F在直径AB上,且$∠ABC=\frac{π}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com