
ΓΨΧβΡΩΓΩΡ≥Μ·Ή±ΤΖ…ζ≤ζΤσ“ΒΈΣΝΥ’Φ”–ΗϋΕύΒΡ –≥ΓΖίΕνΘ§Ρβ‘Ύ2010Ρξ ά≤©ΜαΤΎΦδΫχ––“ΜœΒΝ–¥ΌœζΜνΕ·Θ§Ψ≠Ιΐ –≥ΓΒς≤ιΚΆ≤βΥψΘ§Μ·Ή±ΤΖΒΡΡξœζΝΩxΆρΦΰ”κΡξ¥ΌœζΖ―tΆρ‘Σ÷°Φδ¬ζΉψ3©¹x”κt+1≥…Ζ¥±»άΐΘ§»γΙϊ≤ΜΗψ¥ΌœζΜνΕ·Θ§Μ·Ή±ΤΖΒΡΡξœζΝΩ÷ΜΡή «1ΆρΦΰΘ§“―÷Σ2010Ρξ…ζ≤ζΜ·Ή±ΤΖΒΡ…η±Η’έΨ…ΓΔΈ§–όΒ»ΙΧΕ®Ζ―”ΟΈΣ3Άρ‘ΣΘ§ΟΩ…ζ≤ζ1ΆρΦΰΜ·Ή±ΤΖ–η“Σ‘ΌΆΕ»κ32Άρ‘ΣΒΡ…ζ≤ζΖ―”ΟΘ§»τΫΪΟΩΦΰΜ·Ή±ΤΖΒΡ έΦέΕ®ΈΣΘΚΤδ…ζ≤ζ≥…±ΨΒΡ150%”κΤΫΨυΟΩΦΰ¥ΌœζΖ―ΒΡ“ΜΑκ÷°ΚΆΘ§‘ρΒ±Ρξ…ζ≤ζΒΡΜ·Ή±ΤΖ’ΐΚΟΡήœζΆξΘ°
Θ®1Θ©ΫΪ2010Ρξάϊ»σyΘ®Άρ‘ΣΘ©±μ ΨΈΣ¥ΌœζΖ―tΘ®Άρ‘ΣΘ©ΒΡΚ· ΐΘΜ
Θ®2Θ©ΗΟΤσ“Β2010ΡξΒΡ¥ΌœζΖ―ΆΕ»κΕύ…ΌΆρ‘Σ ±Θ§Τσ“ΒΒΡΡξάϊ»σΉν¥σΘΩ
Θ®ΉΔΘΚάϊ»σ=œζ έ ’»κ©¹…ζ≤ζ≥…±Ψ©¹¥ΌœζΖ―Θ§…ζ≤ζ≥…±Ψ=ΙΧΕ®Ζ―”Ο+…ζ≤ζΖ―”ΟΘ©
ΓΨ¥πΑΗΓΩ
Θ®1Θ©ΫβΘΚ”…Χβ“βΘΚ ![]() Θ§
Θ§
«“Β±t=0 ±Θ§x=1Θ°
Υυ“‘k=2Θ§Φ¥ ![]() Θ°
Θ°
Β±ΡξœζΝΩΈΣxΆρΦΰ ±Θ§≥…±ΨΈΣ3+32xΘ®Άρ‘ΣΘ©Θ°
Μ·Ή±ΤΖΒΡ έΦέΈΣ ![]() Θ®Άρ‘Σ/ΆρΦΰΘ©
Θ®Άρ‘Σ/ΆρΦΰΘ©
Υυ“‘Ρξάϊ»σy= ![]() Θ®Άρ‘ΣΘ©
Θ®Άρ‘ΣΘ©
Α― ![]()
¥ζ»κ’ϊάμΒΟΒΫ ![]() Θ§Τδ÷–tΓί0Θ°
Θ§Τδ÷–tΓί0Θ°
Θ®2Θ©ΫβΘΚ»ΞΖ÷ΡΗ’ϊάμΒΟΒΫΘΚt2+2Θ®y©¹49Θ©t+2y©¹35=0Θ°
ΗΟΙΊ”ΎtΒΡΖΫ≥Χ‘Ύ[0Θ§+ΓόΘ©…œ”–ΫβΘ°
Β±2y©¹35Γή0Θ§Φ¥yΓή17.5 ±Θ§±Ί”–“ΜΫβΘ°
Β±2y©¹35ΘΨ0 ±Θ§ΗΟΙΊ”ΎtΒΡΖΫ≥Χ±Ί–κ”–ΝΫ’ΐΗυ
Υυ“‘ 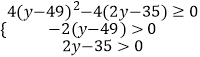 Θ°ΫβΒΟΘΚ17.5ΘΦyΓή42Θ°
Θ°ΫβΒΟΘΚ17.5ΘΦyΓή42Θ°
Ήέ…œΘ§Ρξάϊ»σΉν¥σΈΣ42Άρ‘ΣΘ§¥Υ ±¥ΌœζΖ―t=7Θ®Άρ‘ΣΘ©Θ°
Υυ“‘Β±¥ΌœζΖ―Ε®‘Ύ7Άρ‘Σ ±Θ§Τσ“ΒΒΡΡξάϊ»σΉν¥σΘ°
ΓΨΫβΈωΓΩΘ®1Θ©ΗυΨίΧβ“βΘ§3©¹x”κt+1≥…Ζ¥±»άΐΘ§Ν–≥ωΙΊœΒ ΫΘ§»ΜΚσΗυΨίΒ±t=0 ±Θ§x=1Θ§«σ≥ωkΒΡ÷ΒΘ§Ά®Ιΐx±μ Ψ≥ωΡξάϊ»σyΘ§≤ΔΜ·ΦρΘ§¥ζ»κ’ϊάμΦ¥Ω…«σ≥ωyΆρ‘Σ±μ ΨΈΣ¥ΌœζΖ―tΆρ‘ΣΒΡΚ· ΐΘ°Θ®2Θ©ΗυΨί“―÷Σ¥ζ»κΘ®1Θ©ΒΡΚ· ΐΘ§Ζ÷±πΫχ––Μ·ΦρΘ§άϊ”ΟΙΊ”ΎtΒΡΖΫ≥Χ±Ί–κ”–ΝΫ’ΐΗυΫ®ΝΔΙΊœΒ ΫΘ§Ω…«σ≥ωΉν÷ΒΘ§Φ¥¥ΌœζΖ―ΆΕ»κΕύ…ΌΆρ‘Σ ±Θ§Τσ“ΒΒΡΡξάϊ»σΉν¥σΘ°


 ’ψ¥σ”≈―ß–Γ―ßΡξΦΕœΈΫ”ΫίΨΕ’ψΫ≠¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
’ψ¥σ”≈―ß–Γ―ßΡξΦΕœΈΫ”ΫίΨΕ’ψΫ≠¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…η ΐΝ–{an} «ΙΪ±»¥σ”Ύ1ΒΡΒ»±» ΐΝ–Θ§SnΈΣ ΐΝ–{an}ΒΡ«ΑnœνΚΆΘ§“―÷ΣS3=7Θ§«“a1+3Θ§3a2 Θ§ a3+4ΙΙ≥…Β»≤ν ΐΝ–Θ°
Θ®1Θ©«σ ΐΝ–{an}ΒΡΆ®œνΙΪ ΫΘΜ
Θ®2Θ©«σ ΐΝ–{an+log2an}Θ®nΓ N*Θ©ΒΡ«Α10œνΚΆT10 Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣnΓ N* Θ§ …ηSn «ΒΞΒςΒίΦθΒΡΒ»±» ΐΝ–{an}ΒΡ«ΑnœνΚΆΘ§a1= ![]() «“S2+a2 Θ§ S4+a4 Θ§ S3+a3≥…Β»≤ν ΐΝ–Θ°
«“S2+a2 Θ§ S4+a4 Θ§ S3+a3≥…Β»≤ν ΐΝ–Θ°
Θ®1Θ©«σ ΐΝ–{an}ΒΡΆ®œνΙΪ ΫΘΜ
Θ®2Θ©Φ« ΐΝ–{nan}ΒΡ«ΑnœνΚΆΈΣTn Θ§ «σ÷ΛΘΚΕ‘”Ύ»Έ“β’ΐ’ϊ ΐnΘ§ ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ”κ‘≤Θ®x©¹3Θ©2+Θ®y©¹3Θ©2=8œύ«–Θ§«“‘ΎxΓΔy÷α…œΫΊΨύœύΒ»ΒΡ÷±œΏ”–Θ® Θ©
A.4Χθ
B.3Χθ
C.2Χθ
D.1Χθ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΥδ»ΜΈϋ―Χ”–ΚΠΫΓΩΒΘ§ΒΪ «”…”Ύάζ Ζ“‘ΦΑ…γΜαΒΡ‘≠“ρΘ§Έϋ―Χ“≤ «≤ΩΖ÷ΙΪΟώΫΜΦ ΒΡ÷Ί“ΣΟΫΫιΘ° άΫγΈά…ζΉι÷·1987Ρξ11‘¬Ϋ®“ιΑ―ΟΩΡξΒΡ4‘¬7»’Ε®ΈΣ άΫγΈό―Χ»’Θ§«“¥”1989ΡξΩΣ ΦΘ§ άΫγΈό―Χ»’ΗΡΈΣΟΩΡξΒΡ5‘¬31»’Θ°Ρ≥±®…γΦ«’ΏΉ®Ο≈Ε‘Έϋ―ΧΒΡ –ΟώΉωΝΥΫδ―ΧΖΫΟφΒΡΒς≤ιΘ§Ψ≠≥ι―υ÷Μ”–![]() ΒΡ―ΧΟώ±μ Ψ‘Η“βΫδ―ΧΘ§ΫΪΤΒ¬ ”ΈΣΗ≈¬ Θ°
ΒΡ―ΧΟώ±μ Ψ‘Η“βΫδ―ΧΘ§ΫΪΤΒ¬ ”ΈΣΗ≈¬ Θ°
Θ®1Θ©¥”ΗΟ –Έϋ―ΧΒΡ –Οώ÷–ΥφΜζ≥ι»Γ3ΈΜΘ§«σ÷Ν…Ό”–“ΜΈΜ―ΧΟώ‘Η“βΫδ―ΧΒΡΗ≈¬ ΘΜ
Θ®2Θ©¥”ΗΟ –Έϋ―ΧΒΡ –Οώ÷–ΥφΜζ≥ι»Γ4ΈΜΘ§ ![]() ±μ Ψ‘Η“βΫδ―ΧΒΡ»Υ ΐΘ§«σ
±μ Ψ‘Η“βΫδ―ΧΒΡ»Υ ΐΘ§«σ![]() ΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊΘ°
ΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ°
Θ°
Θ®1Θ©Β±![]() ±Θ§«σΚ· ΐ
±Θ§«σΚ· ΐ![]() ΒΡΒΞΒς«χΦδΘΜ
ΒΡΒΞΒς«χΦδΘΜ
Θ®2Θ©»τΚ· ΐ![]() Φ»”–“ΜΗωΦΪ–Γ÷Β”÷”–“ΜΗωΦΪ¥σ÷ΒΘ§«σ
Φ»”–“ΜΗωΦΪ–Γ÷Β”÷”–“ΜΗωΦΪ¥σ÷ΒΘ§«σ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©»τ¥φ‘Ύ![]() Θ§ ΙΒΟΒ±
Θ§ ΙΒΟΒ±![]() ±Θ§
±Θ§ ![]() ΒΡ÷Β”ρ «
ΒΡ÷Β”ρ «![]() Θ§«σ
Θ§«σ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘≤x2+y2©¹2x+4y+3=0ΒΡ‘≤–ΡΒΫ÷±œΏx©¹y=1ΒΡΨύάκΈΣΘΚΘ® Θ©
A.2
B.![]()
C.1
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΥΡάβΉΕ![]() ÷–Θ§ΥΡ±Ώ–Έ
÷–Θ§ΥΡ±Ώ–Έ![]() «Νβ–ΈΘ§
«Νβ–ΈΘ§ ![]() Θ§”÷
Θ§”÷![]() ΤΫΟφ
ΤΫΟφ![]() ,
,
Βψ![]() «άβ
«άβ![]() ΒΡ÷–ΒψΘ§
ΒΡ÷–ΒψΘ§ ![]() ‘Ύάβ
‘Ύάβ![]() …œΘ§«“
…œΘ§«“![]() .
.
Θ®1Θ©÷ΛΟςΘΚΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©»τ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§«σΥΡάβΉΕ
Θ§«σΥΡάβΉΕ![]() ΒΡΧεΜΐ.
ΒΡΧεΜΐ.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com