
分析 (1)由题意画出图形,利用$\frac{y-1}{x}$的几何意义,即圆上动点与定点(0,1)的斜率求答案;
(2)|x+y+l|=$\sqrt{2}•\frac{|x+y+1|}{\sqrt{2}}$,$\frac{|x+y+1|}{\sqrt{2}}$的几何意义为圆上的动点到直线x+y+1=0的距离.圆心到直线的距离加上半径为最大值,圆心到直线的距离减半径长为最小值,则答案可求.
解答 解:(1)(x-2)2+(y-2)2=1表示以(2,2)为圆心,以1为半径的圆,
而$\frac{y-1}{x}$的几何意义为圆上动点与定点(0,1)的斜率,
如图,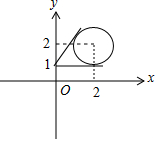
设过(0,1)且与圆相切的直线方程为y=kx+1,即kx-y+1=0.
由圆心(2,2)到直线kx-y+1=0的距离d=$\frac{|2k-2+1|}{\sqrt{{k}^{2}+1}}=1$,解得k=0或k=$\frac{4}{3}$.
∴$\frac{y-1}{x}$∈[0,$\frac{4}{3}$];
(2)|x+y+l|=$\sqrt{2}•\frac{|x+y+1|}{\sqrt{2}}$,$\frac{|x+y+1|}{\sqrt{2}}$的几何意义为圆上的动点到直线x+y+1=0的距离.
圆心到直线的距离加上半径为最大值,圆心到直线的距离减半径长为最小值,
由此$\frac{|x+y+1|}{\sqrt{2}}$∈[$\frac{5}{\sqrt{2}}-1,\frac{5}{\sqrt{2}}+1$],则|x+y+l|∈[5-$\sqrt{2}$,5+$\sqrt{2}$].
点评 本题考查圆的标准方程,考查了数学转化思想方法和数形结合的解题思想方法,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 不充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x=-\frac{1}{8}$ | B. | $y=-\frac{1}{8}$ | C. | $y=-\frac{1}{4}$ | D. | $y=-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
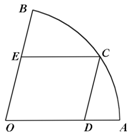 如图,某观光休闲庄园内有一块扇形花卉园OAB,其中O为扇形所在圆的圆心,扇形半径为500米,cos∠AOB=$\frac{1}{4}$.庄园经营者欲在花卉园内修建一条赏花长廊,分别在边OA、弧$\widehat{AB}$、边OB上选点D,C,E修建赏花长廊CD,CE,且CD∥OB,CE∥OA,设CD长为x米,CE长为y米.
如图,某观光休闲庄园内有一块扇形花卉园OAB,其中O为扇形所在圆的圆心,扇形半径为500米,cos∠AOB=$\frac{1}{4}$.庄园经营者欲在花卉园内修建一条赏花长廊,分别在边OA、弧$\widehat{AB}$、边OB上选点D,C,E修建赏花长廊CD,CE,且CD∥OB,CE∥OA,设CD长为x米,CE长为y米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
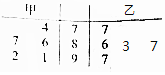 某工厂组织工人技能培训,其中甲、乙两名技工在培训时进行的5次技能测试中的成绩如图茎叶图所示.
某工厂组织工人技能培训,其中甲、乙两名技工在培训时进行的5次技能测试中的成绩如图茎叶图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com