
分析 设Q(x,y),M(s,t),则N(0,t),由于向量$\overrightarrow{OQ}=\overrightarrow{OM}+\overrightarrow{ON}$,利用向量相等可得$\left\{\begin{array}{l}{x=s}\\{y=2t}\end{array}\right.$,解出s,t再代入圆的方程即可.
解答 解:设Q(x,y),M(s,t),则N(0,t),s2+t2=9.(*)
∵向量$\overrightarrow{OQ}=\overrightarrow{OM}+\overrightarrow{ON}$,(O为原点),∴$\left\{\begin{array}{l}{x=s}\\{y=2t}\end{array}\right.$,
解得$\left\{\begin{array}{l}{s=x}\\{t=y}\end{array}\right.$,代入(*)化为$\frac{x^2}{4}+{y^2}=9$.
故答案为$\frac{x^2}{4}+{y^2}=9$.
点评 本题考查了轨迹方程,考查代点法,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | m<p<q<n | B. | p<m<q<n | C. | m<p<n<q | D. | p<m<n<q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
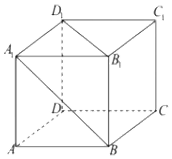
| A. | A1B∥D1B | B. | AC1⊥B1C | ||
| C. | A1B与平面DBD1B1成角为45° | D. | A1B,B1C成角为30° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | $\sqrt{6}$ | C. | 3 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3,6} | B. | {5} | C. | {2,4} | D. | {2,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±2x | B. | y=±$\frac{1}{4}$x | C. | y=±$\frac{1}{2}$x | D. | y=±$\frac{{\sqrt{2}}}{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com