
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,A1D与AD1交于点E,AA1=AD=2AB=4.
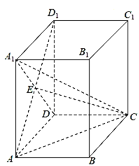
(1)证明:AE⊥平面ECD;
(2)求点C1到平面AEC的距离.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由四边形ABCD是矩形,得到CD⊥AD,再由面面垂直的性质,证得CD⊥AE,结合线面垂直的判定定理,即可得到AE⊥平面ECD.;
(2)连接CD1,得到点C1到平面AEC的距离即为点C1到平面ACD1的距离, 利用“等体积法”,结合V![]() ,即可求得点C1到平面AEC的距离.
,即可求得点C1到平面AEC的距离.
(1)∵四边形ABCD是矩形,∴CD⊥AD,
∵AA1⊥平面ABCD,CD平面ABCD,∴AA1⊥CD,
又AA1∩AD=A,∴CD⊥平面ADD1A1,∴CD⊥AE,
∵四边形ADD1A1是平行四边形,∴E是A1D的中点,
∵AA1=AD,∴AE⊥DE,又CD∩DE=D,∴AE⊥平面ECD.
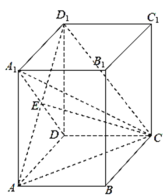
(2)连接CD1,则点C1到平面AEC的距离即为点C1到平面ACD1的距离,
在△ACD1中,AC=2![]() ,AD1=4
,AD1=4![]() ,CD1=2
,CD1=2![]() ,
,
∴CE⊥AD1,且CE![]() 2
2![]() ,
,
∴S![]() 4
4![]() ,
,
设C1到平面ACD1的距离为h,则V![]() ,
,
又V![]() ,
,
所以4![]() h=16,即h
h=16,即h![]() ,∴点C1到平面AEC的距离为
,∴点C1到平面AEC的距离为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知鲜切花![]() 的质量等级按照花枝长度
的质量等级按照花枝长度![]() 进行划分,划分标准如下表所示.
进行划分,划分标准如下表所示.
花枝长度 |
|
|
|
鲜花等级 | 三级 | 二级 | 一级 |
某鲜切花加工企业分别从甲乙两个种植基地购进鲜切花![]() ,现从两个种植基地购进的鲜切花
,现从两个种植基地购进的鲜切花![]() 中分别随机抽取30个样品,测量花枝长度并进行等级评定,所抽取样品数据如图所示.
中分别随机抽取30个样品,测量花枝长度并进行等级评定,所抽取样品数据如图所示.
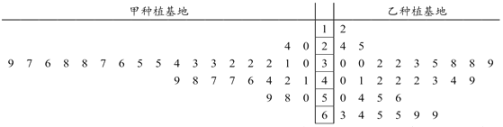
(1)根据茎叶图比较两个种植基地鲜切花![]() 的花枝长度的平均值及分散程度(不要求计算具体值,给出结论即可);
的花枝长度的平均值及分散程度(不要求计算具体值,给出结论即可);
(2)若从等级为三级的样品中随机选取2个进行新产品试加工,求选取的2个全部来自乙种植基地的概率;
(3)根据该加工企业的加工和销售记录,了解到来自乙种植基地的鲜切花![]() 的加工产品的单件利润为4元;来自乙种植基地的鲜切花
的加工产品的单件利润为4元;来自乙种植基地的鲜切花![]() 的加工产品的单件成本为10元,销售率(某等级产品的销量与产量的比值)及单价如下表所示.
的加工产品的单件成本为10元,销售率(某等级产品的销量与产量的比值)及单价如下表所示.
三级花加工产品 | 二级花加工产品 | 一级花加工产品 | |
销售率 |
|
|
|
单价/(元/件) | 12 | 16 | 20 |
由于鲜切花![]() 加工产品的保鲜特点,未售出的产品均可按原售价的50%处理完毕.用样本估计总体,如果仅从单件产品的利润的角度考虑,该鲜切花加工企业应该从哪个种植基地购进鲜切花
加工产品的保鲜特点,未售出的产品均可按原售价的50%处理完毕.用样本估计总体,如果仅从单件产品的利润的角度考虑,该鲜切花加工企业应该从哪个种植基地购进鲜切花![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年新型冠状病毒肺炎(简称“新冠肺炎”)成为威胁全球的公共卫生问题,中医药在本次新冠肺炎的治疗中发挥了重要作用.研究人员对66例普通型新冠肺炎恢复期患者进行了中医临床特征分析,发现主要证型有气阴两虚证与肺脾气虚证,同时可能兼夹湿证.为研究这两种主要证型在兼夹湿证的难易上是否有差异,研究人员将湿证症状分级量化,将所有肺脾气虚证患者的量化分作成茎叶图.
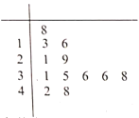
(1)若量化分不低于16分,即可诊断为兼夹湿证,请参考茎叶图,完成下面![]() 列联表.
列联表.
夹湿证 | 非夹湿证 | 合计 | |
气阴两虚 | 20 | ||
肺脾气虚 | |||
合计 | 66 |
(2)根据此资料,能否有99%的把握认为两种主要证型在兼夹湿证的难易上有差异?
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
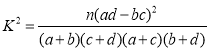
查看答案和解析>>
科目:高中数学 来源: 题型:
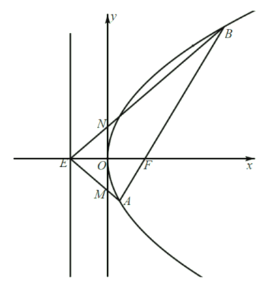
【题目】如图,抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 是抛物线的准线与
是抛物线的准线与![]() 轴的交点,直线
轴的交点,直线![]() 经过焦点
经过焦点![]() 且与抛物线相交于
且与抛物线相交于![]() 、
、![]() 两点,直线
两点,直线![]() 、
、![]() 分别交
分别交![]() 轴于
轴于![]() 、
、![]() 两点,记
两点,记![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() .
.
(1)求证: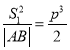 ;
;
(2)若![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆P经过点![]() ,并且与圆
,并且与圆![]() 相切.
相切.
(Ⅰ)求圆心P的轨迹C的方程;
(Ⅱ)O是坐标原点,过点![]() 的直线
的直线![]() 与C交于A,B两点,在C上是否存在点Q,使得四边形
与C交于A,B两点,在C上是否存在点Q,使得四边形![]() 是平行四边形?
是平行四边形?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直角梯形ABCD中,![]() ,
,![]() ,
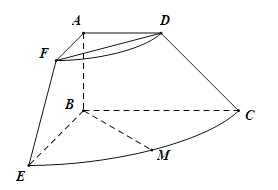
,![]() ,将直角梯形ABCD(及其内部)以AB所在直线为轴顺时针旋转90°,形成如图所示的几何体,其中M为
,将直角梯形ABCD(及其内部)以AB所在直线为轴顺时针旋转90°,形成如图所示的几何体,其中M为![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)求异面直线BM与EF所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】勒洛三角形是具有类似圆的“定宽性”的曲线,它是由德国机械工程专家、机构运动学家勒洛首先发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形.如图中的两个勒洛三角形,它们所对应的等边三角形的边长比为![]() ,若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率是( )
,若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.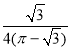
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com