
| A. | (0,1] | B. | (0,1) | C. | (0,2) | D. | (0,2] |
分析 令x=y,可得f(x2)+f(2x)≥f2(x),即有ax4+b+4ax2+b≥a2x4+2abx2+b2,即为(a-a2)x4+(4a-2ab)x2+2b-b2≥0,讨论二次项的系数为0和大于0,结合单调性,即可得到所求a的范围.
解答 解:令x=y,可得f(x2)+f(2x)≥f2(x),
即有ax4+b+4ax2+b≥a2x4+2abx2+b2,
即为(a-a2)x4+(4a-2ab)x2+2b-b2≥0,
当a-a2=0,即a=1,(4-2b)x2+2b-b2≥0,
当2-b≥0即b≤2时,不等式恒成立;
当a-a2>0,即0<a<1时,2b-b2≥0,即b≤2,
且-$\frac{4a-2ab}{a-{a}^{2}}$≤0,成立.
综上可得a的范围是(0,1).
故选:B.
点评 本题考查二次函数的单调性的运用,同时考查不等式恒成立问题,注意运用分类讨论的思想方法,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | a+b=2c | B. | a+b≤2c | C. | a+b<2c | D. | a+b≥2c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2) | B. | (2,+∞) | C. | (-∞,0) | D. | (-2,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
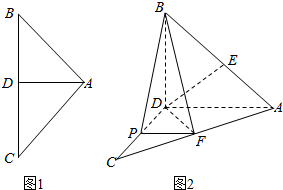 如图1,AD是等腰直角三角形ABC斜边上的高AB=4,沿AD把△ABC的两部分折成直二面角(如图2),P,E,F分别为CD,CA,BA的中点.求证:
如图1,AD是等腰直角三角形ABC斜边上的高AB=4,沿AD把△ABC的两部分折成直二面角(如图2),P,E,F分别为CD,CA,BA的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
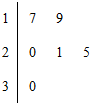 某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为
某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为 | A. | $\frac{8}{15}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45°-4×360° | B. | -45°-4×360° | C. | -45°-5×360° | D. | 315°-5×360° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com