【题目】已知抛物线
的焦点为
，
为坐标原点，过点的直线
与
交于
、
两点.
（1）若直线与圆
相切，求直线的方程；
（2）若直线与
轴的交点为
，且
，
，试探究：
是否为定值.若为定值，求出该定值，若不为定值，试说明理由.
【答案】（1）
；（2）
为定值
.
【解析】
（1）对直线
的斜率是否存在进行分类讨论，由直线与圆
相切，得出圆心到直线的距离等于半径，进而可求得直线的方程；
（2）对直线的斜率是否存在进行分类讨论，可知当直线的斜率不存在时不满足题意，在直线的斜率存在时，设直线的方程为
，与抛物线
的方程联立，列出韦达定理，利用向量的坐标运算得出关于
、
的表达式，代入韦达定理化简计算可求得的值.
（1）由已知得
.
当直线的斜率不存在时，直线的方程为
，此时，直线与圆相交，不合乎题意；
当直线的斜率存在时，设直线的方程为，即
，
由直线与圆
相切，得
，解得
.
综上所述，直线的方程为；
（2）当直线的斜率不存在时，直线的方程为，则直线与抛物线只有一个交点，不合乎题意；
当直线与
轴不重合时，设直线的方程为，设
、
.
若
，则直线与轴平行，不合乎题意，所以
.
联立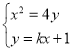
，消去
并整理得
，由韦达定理得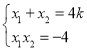
，
易知
，由
，得
，
则
，
，同理可得
，
所以
，
所以为定值.
学而优衔接教材南京大学出版社系列答案科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，曲线C的参数方程为
（
为参数，
）.以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的圾坐标方
，且直线l与曲线C相交于A，B两点.
（1）求曲线C的普通方程和l的直角坐标方程；
（2）若
，点
满足
，求此时r的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
，设函数
，
．
（1）试讨论
的单调性；
（2）设函数
，是否存在实数
，使得
存在两个极值点
，
，且满足
？若存在，求的取值范围；若不存在，请说明理由．
注：
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
（
，
）.
（1）若
，且
在
内有且只有一个零点，求的值；
（2）若
，且有三个不同零点，问是否存在实数使得这三个零点成等差数列？若存在，求出的值，若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，曲线C的参数方程为
，（θ为参数），以原点为极点，x轴非负半轴为极轴建立极坐标系．
（1）求曲线C的极坐标方程；
（2）在平面直角坐标系xOy中，A（﹣2，0），B（0，﹣2），M是曲线C上任意一点，求△ABM面积的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
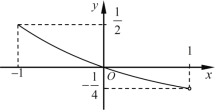
【题目】函数
的定义域为
，其图象如图所示．函数
是定义域为
的奇函数，满足
，且当
时，
．给出下列三个结论：
①
；
②函数在
内有且仅有
个零点；
③不等式
的解集为
．
其中，正确结论的序号是________．
查看答案和解析>>
科目：高中数学 来源： 题型：
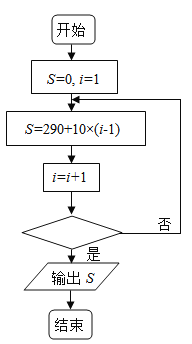
【题目】《九章算术》中盈不足章中有这样一则故事：“今有良马与驽马发长安，至齐. 齐去长安三千里. 良马初日行一百九十三里，日增一十二里；驽马初日行九十七里，日减二里．” 为了计算每天良马和驽马所走的路程之和，设计框图如下图. 若输出的 
的值为 350，则判断框中可填（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，已知定点
，点A在x轴的非正半轴上运动，点B在y轴上运动，满足
，A关于点B的对称点为M，设点M的轨迹为曲线C.
（1）求C的方程；
（2）已知点
，动直线
与C相交于P，Q两点，求过G，P，Q三点的圆在直线
上截得的弦长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
