
 在如图所示的平面中,点C为半圆的直径AB延长线上的一点,AB=BC=2,过动点P作半圆的切线PQ,若PC=$\sqrt{2}$PQ,则△PAC的面积的最大值为4$\sqrt{5}$.
在如图所示的平面中,点C为半圆的直径AB延长线上的一点,AB=BC=2,过动点P作半圆的切线PQ,若PC=$\sqrt{2}$PQ,则△PAC的面积的最大值为4$\sqrt{5}$. 分析 以AB所在直线为x轴,以AB的垂直平分线为y轴,建立平面直角坐标系,利用两点间距离公式推导出点P的轨迹方程是以(-3,0)为圆心,以r=2$\sqrt{5}$为半径的圆,由此能求出△PAC的面积的最大值.
解答  解:以AB所在直线为x轴,以AB的垂直平分线为y轴,
解:以AB所在直线为x轴,以AB的垂直平分线为y轴,
建立平面直角坐标系,
∵AB=BC=2,∴C(3,0),
设P(x,y),
∵过动点P作半圆的切线PQ,PC=$\sqrt{2}$PQ,
∴$\sqrt{(x-3)^{2}+{y}^{2}}$=$\sqrt{2}$•$\sqrt{{x}^{2}+{y}^{2}-1}$,
整理,得x2+y2+6x-11=0,
∴点P的轨迹方程是以(-3,0)为圆心,以r=2$\sqrt{5}$为半径的圆,
∴当点P在直线x=-3上时,△PAC的面积的最大,
∴(S△PAC)max=$\frac{1}{2}×4×2\sqrt{5}$=4$\sqrt{5}$.
故答案为:4$\sqrt{5}$.
点评 本题考查三角形面积的最大值的求法,是中档题,解题时要认真审题,注意两点间距离公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $y=±\frac{{\sqrt{2}}}{2}x$ | B. | $y=±\sqrt{2}x$ | C. | y=±2x | D. | $y=±\frac{1}{2}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)<f($\frac{5}{2}$)<f($\frac{7}{2}$) | B. | f($\frac{7}{2}$)<f(1)<f($\frac{5}{2}$) | C. | f($\frac{7}{2}$)<f($\frac{5}{2}$)<f(1) | D. | f($\frac{5}{2}$)<f(1)<f($\frac{7}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
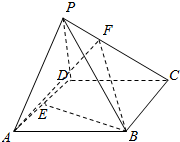 如图所示,P为?ABCD所在平面外一点,E为AD的中点,F为PC上一点,当PA∥平面EBF时,$\frac{PF}{FC}$=$\frac{1}{2}$.
如图所示,P为?ABCD所在平面外一点,E为AD的中点,F为PC上一点,当PA∥平面EBF时,$\frac{PF}{FC}$=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 我校为进行“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S(平方米)的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上.已知∠ACB=60°,|AC|=30米,|AM|=x米,x∈[10,20].设矩形AMPN健身场地每平方米的造价为$\frac{37k}{{\sqrt{S}}}$元,再把矩形AMPN以外(阴影部分)铺上草坪,每平方米的造价为$\frac{12k}{{\sqrt{S}}}$元(k为正常数).
我校为进行“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S(平方米)的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上.已知∠ACB=60°,|AC|=30米,|AM|=x米,x∈[10,20].设矩形AMPN健身场地每平方米的造价为$\frac{37k}{{\sqrt{S}}}$元,再把矩形AMPN以外(阴影部分)铺上草坪,每平方米的造价为$\frac{12k}{{\sqrt{S}}}$元(k为正常数).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com