[题目]已知向量. .设函数.且的图象过点和点.(Ⅰ)求的值,(Ⅱ)将的图象向左平移()个单位后得到函数的图象.若的图象上各最高点到点的距离的最小值为1.求的单调增区间. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知向量，，设函数，且的图象过点和点.

（Ⅰ）求的值；

（Ⅱ）将的图象向左平移（）个单位后得到函数的图象.若的图象上各最高点到点的距离的最小值为1，求的单调增区间.

【答案】（I）.

（II）函数的单调递增区间为.

【解析】试题分析：（Ⅰ）利用向量的数量积坐标运算公式代入函数式整理化简，将函数过的点和点代入就可得到关于的方程，解方程求其值；（Ⅱ）利用图像平移的方法得到的解析式，利用最高点到点的距离的最小值为1求得角，得，求减区间需令解的范围

试题解析：（1）由题意知．

的过图象过点和，

所以即解得

（2）由（1）知．

由题意知．

设的图象上符合题意的最高点为，

由题意知，所以，即到点（0，3）的距离为1的最高点为（0，2）．

将其代入得，因为，所以，

因此．

由Z得Z，

所以函数的单调递增区间为

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】一企业从某生产线上随机抽取件产品，测量这些产品的某项技术指标值，得到的频率分布直方图如图.

（1）估计该技术指标值平均数；

（2）在直方图的技术指标值分组中，以落入各区间的频率作为取该区间值的频率，若，则产品不合格，现该企业每天从该生产线上随机抽取件产品检测，记不合格产品的个数为，求的数学期望.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E、F分别是AC、AD上的动点，且

（1）求证：不论为何值，总有平面BEF⊥平面ABC；

（2）当λ为何值时，平面BEF⊥平面ACD ?

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图：

记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用（单位：元）, 表示购机的同时购买的易损零件数.

（Ⅰ）若=19,求y与x的函数解析式；

（Ⅱ）若要求“需更换的易损零件数不大于”的频率不小于0.5,求的最小值；

（Ⅲ）假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】（本小题满分12分）下图是某市今年1月份前30天空气质量指数（AQI）的趋势图.

（1）根据该图数据在答题卷中完成频率分布表，并在图中补全这些数据的频率分布直方图；

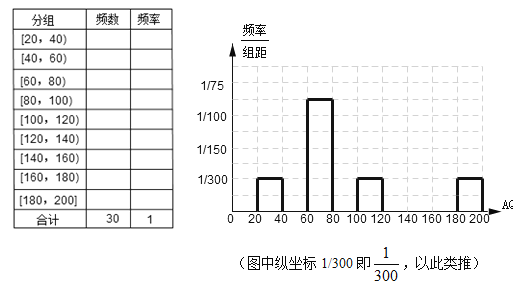
（2）当空气质量指数（AQI）小于100时，表示空气质量优良．某人随机选择当月（按30天计）某一天

到达该市，根据以上信息，能否认为此人到达当天空气质量优良的可能性超过60%？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知=（）．

(Ⅰ)当=2时，求函数在（1，）处的切线方程；

(Ⅱ)若≥1时，≥0，求实数的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在贵阳市创建全国文明城市工作验收时，国家文明委有关部门对我校高二年级6名学生进行了问卷调查，6人得分情况如下：5,6,7,8,9,10.把这6名学生的得分看成一个总体．如果用简单随机抽样方法从这6名学生中抽取2名，他们的得分组成一个样本，则该样本平均数与总体平均数之差的绝对值不超过0.5的概率为(　　)

A.； B.； C.； D..