
����Ŀ��������ŷɴ��ɹ�����˵�һ�����˺�����У�ʵ�����й�����ĺ������룬ij��ʱ��ɴ���̫�������еĹ����һ����Բ����������Բ��һ�������ϣ���ͼ��ʾ�����躽��Ա�������������Ϊd1 �� ��������Զ����Ϊd2 �� ����İ뾶ΪR�������������һ��������������������۷ɴ����й��������һ�������ϣ�����ס��һ�����ɷ���ij�������ź���Ҫ�����еĺ���Ա��ת������˲��ܽ��յ����������źŴ�������̾���Ϊ�� �� 
A.d1+d2+R
B.d2��d1+2R
C.d2+d1��2R
D.d1+d2
 ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д� Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д� ������������Ծ�ϵ�д�
������������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�������80��ѧ�������о�ѧ��������ë���˶����Ա�Ĺ�ϵ���õ������![]() ��������
��������
��1������������Ƶ����Ϊ����ĸ��ʣ�������鱾У��3��ѧ��������3���а�����ë���˶�������Ϊ![]() ����
����![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
��2�����ݱ�3�����ݣ��ܷ���Ϊ������ë���˶����Ա��йأ�
����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֲ�Ʒ�Ĺ�����֧��![]() �����۶�
�����۶�![]() ֮�������µĶ�Ӧ���ݣ���λ����Ԫ����
֮�������µĶ�Ӧ���ݣ���λ����Ԫ����
![]()
��1����![]() ����
����![]() �����Իع�ֱ�߷��̣�
�����Իع�ֱ�߷��̣�
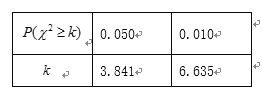
��2���ݴ˹��ƹ�����Ϊ10��Ԫʱ��������![]() ��ֵ.
��ֵ.
�������������Իع鷽��![]() ������
������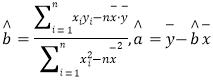 ��
��
�ο���ʽ: 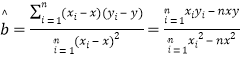
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ACDE���ڵ�ƽ����ƽ��ABC��ֱ��M��CE��AD�Ľ��㣬AC![]() BC,��AC=BC.
BC,��AC=BC.
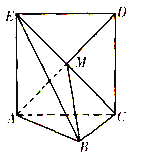
(1)��֤��AM![]() ƽ��EBC��
ƽ��EBC��
(2)��ֱ��AB��ƽ��EBC���ɽǵĴ�С��
(3)������A-BE-C�Ĵ�С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=��a+1��lnx��x2 �� ![]() ��
��
��1�����ۺ���f��x���ĵ������䣻
��2��������f��x����g��x���ڣ�0��+�ޣ��ϵĵ����������෴�� ������ ![]() ������ʽ
������ʽ ![]() ���������ʵ��t��ȡֵ��Χ��
���������ʵ��t��ȡֵ��Χ��
������h��x��=xg��x����f��x��������ʵ��x1��x2����h��x1��+h��x2��+6x1x2=6��֤��0��x1+x2��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
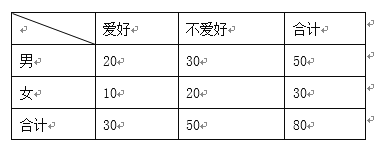
����Ŀ��Ϊ�������Թ��ȵķ��ز��г����е��ؾ��ߣ�ͳ�Ʋ��ŶԳ����˺�ũ���˽�����������Ԥ����У��ü���������ķ�����ȡ��110�˽���ͳ�ƣ��õ�������������
�� | ���� | ���� | |
������ | 5 | 15 | |
ũ���� | 20 | 10 |
��֪�����г���������ũ������֮����3��8��
���ֱ��������г������еIJ���������ũ�����еľ���������
���Ӳ�����еij��������÷ֲ����������ȡ6�ˣ���һ��ͳ�Ƴ����˵�ij������ָ�꣬����һ�����˵�ָ������3��һ�������˵�ָ������2��һ�������˵�ָ������1�����ڴ���6���������ѡȡ3�ˣ���X=�ٳ�ȡ3��ָ��֮�ͣ���X�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�Ӹ�һ�꼶ѧ���������ȡ40��ѧ���������ǵ����п�����ѧ�ɼ�������100�֣��ɼ���Ϊ������40�ֵ��������ֳ����Σ�[40��50����[50��60��������[90��100]��õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ������ǰ���ε�Ƶ�ʳɵȱ����У� 
��1����ͼ��ʵ��a��ֵ��
��2������У��һ�꼶����ѧ��640�ˣ��Թ��Ƹ�У��һ�꼶���п�����ѧ�ɼ�������80�ֵ�������
��3��������������ѧ�ɼ���[40��50����[90��100]�����������ڵ�ѧ�������ѡȡ����ѧ������������ѧ���ɼ���[90��100]�ڵ�����ΪX�����������X�ķֲ��к�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=e2x �� g��x��=kx+1��k��R���� ������ֱ��y=g��x���ͺ���y=f��x����ͼ�����У���k��ֵ��
����k��0ʱ����������ʵ��m��ʹ������x�ʣ�0��m��������|f��x����g��x��|��2x���������k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=|2ax+1|����a��R��������ʽf��x����3�Ľ⼯{x|��2��x��1}��
��1����a��ֵ��
��2���� ![]() ���������k��ȡֵ��Χ��
���������k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com