
【题目】2020年是我国全面建成小康社会和“十三五”规划收官之年,也是佛山在经济总量超万亿元新起点上开启发展新征程的重要历史节点.作为制造业城市,佛山一直坚持把创新摆在制造业发展全局的前置位置和核心位置,聚焦打造成为面向全球的国家制造业创新中心,走“世界科技+佛山智造+全球市场”的创新发展之路.在推动制造业高质量发展的大环境下,佛山市某工厂统筹各类资源,进行了积极的改革探索.下表是该工厂每月生产的一种核心产品的产量x(![]() )(件)与相应的生产总成本y(万元)的四组对照数据.
)(件)与相应的生产总成本y(万元)的四组对照数据.
x | 5 | 7 | 9 | 11 |
y | 200 | 298 | 431 | 609 |
工厂研究人员建立了y与x的两种回归模型,利用计算机算得近似结果如下:
模型①:![]()
模型②:![]() .
.
其中模型①的残差(实际值-预报值)图如图所示:
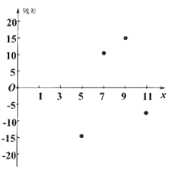
(1)根据残差分析,判断哪一个模型更适宜作为y关于x的回归方程?并说明理由;
(2)市场前景风云变幻,研究人员统计历年的销售数据得到每件产品的销售价格q(万元)是一个与产量x相关的随机变量,分布列为:
q |
|
|
|
P | 0.5 | 0.4 | 0.1 |
结合你对(1)的判断,当产量x为何值时,月利润的预报期望值最大?最大值是多少(精确到0.1)?
【答案】(1)模型①更适宜作为y关于x的回归方程,见解析(2)产量为11件时,月利润的预报期望值最大,最大值是774.8万元.
【解析】
(1)作出模型②的残点图,再对比①的残点图分析即可.
(2)根据题意作出Y的分布列,进而得出其数学期望![]() ,再求导分析其单调性求出最大值即可.
,再求导分析其单调性求出最大值即可.
(1)模型②的残差数据如下表:
x | 5 | 7 | 9 | 11 |
y | 200 | 298 | 431 | 609 |
| 20 |
|
| 21 |
模型②的残点图如图所示.
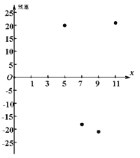
模型①更适宜作为y关于x的回归方程,因为:
理由1:模型①这个4个样本点的残差的绝对值都比模型②的小.
理由2:模型①这4个样本的残差点落在的带状区域比模型②的带状区域更窄.
理由3:模型①这4个样本的残差点比模型②的残差点更贴近x轴.
(2)设月利润为Y,由题意知![]() ,则Y的分布列为:
,则Y的分布列为:
Y |
|
|
|
P | 0.5 | 0.4 | 0.1 |
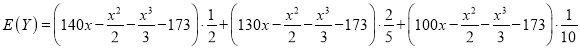
![]() .
.
设函数![]() ,
,![]() ,
,![]() ,
,
令![]() ,解得
,解得![]() 或
或![]() (舍),
(舍),
当![]() 时,
时,![]() ,则
,则![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,则
,则![]() 单调递减.
单调递减.
则函数![]() 的最大值
的最大值![]() ,即产量为11件时,月利润的预报期望值最大,最大值是774.8万元.
,即产量为11件时,月利润的预报期望值最大,最大值是774.8万元.


科目:高中数学 来源: 题型:
【题目】新冠病毒是一种通过飞沫和接触传播的变异病毒,为筛查该病毒,有一种检验方式是检验血液样本相关指标是否为阳性,对于![]() 份血液样本,有以下两种检验方式:一是逐份检验,则需检验
份血液样本,有以下两种检验方式:一是逐份检验,则需检验![]() 次.二是混合检验,将其中
次.二是混合检验,将其中![]() 份血液样本分别取样混合在一起,若检验结果为阴性,那么这
份血液样本分别取样混合在一起,若检验结果为阴性,那么这![]() 份血液全为阴性,因而检验一次就够了;如果检验结果为阳性,为了明确这
份血液全为阴性,因而检验一次就够了;如果检验结果为阳性,为了明确这![]() 份血液究竟哪些为阳性,就需要对它们再逐份检验,此时
份血液究竟哪些为阳性,就需要对它们再逐份检验,此时![]() 份血液检验的次数总共为
份血液检验的次数总共为![]() 次.某定点医院现取得4份血液样本,考虑以下三种检验方案:方案一,逐个检验;方案二,平均分成两组检验;方案三,四个样本混在一起检验.假设在接受检验的血液样本中,每份样本检验结果是阳性还是阴性都是相互独立的,且每份样本是阴性的概率为
次.某定点医院现取得4份血液样本,考虑以下三种检验方案:方案一,逐个检验;方案二,平均分成两组检验;方案三,四个样本混在一起检验.假设在接受检验的血液样本中,每份样本检验结果是阳性还是阴性都是相互独立的,且每份样本是阴性的概率为![]() .
.
(Ⅰ)求把2份血液样本混合检验结果为阳性的概率;
(Ⅱ)若检验次数的期望值越小,则方案越“优”.方案一、二、三中哪个最“优”?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为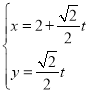 (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为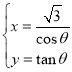 (
(![]() 为参数).
为参数).
(1)求曲线![]() ,
,![]() 的普通方程;
的普通方程;
(2)已知点![]() ,若曲线
,若曲线![]() ,
,![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面内与两定点![]() ,
,![]() 连线的斜率之积等于
连线的斜率之积等于![]() 的点的轨迹,加上
的点的轨迹,加上![]() 、
、![]() 两点所成的曲线为
两点所成的曲线为![]() .若曲线
.若曲线![]() 与
与![]() 轴的正半轴的交点为
轴的正半轴的交点为![]() ,且曲线
,且曲线![]() 上的相异两点
上的相异两点![]() 、
、![]() 满足
满足![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)求![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盒中有形状、大小都相同的2个红色球和3个黄色球,从中取出一个球,观察颜色后放回并往盒中加入同色球4个,再从盒中取出一个球,则此时取出黄色球的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的图象在
的图象在![]() (
(![]() 为自然对数的底数)处的切线方程;
为自然对数的底数)处的切线方程;
(2)若对任意的![]() ,均有
,均有![]() ,则称
,则称![]() 为
为![]() 在区间
在区间![]() 上的下界函数,
上的下界函数,![]() 为
为![]() 在区间
在区间![]() 上的上界函数.
上的上界函数.
①若![]() ,求证:
,求证:![]() 为
为![]() 在
在![]() 上的上界函数;
上的上界函数;
②若![]() ,
,![]() 为
为![]() 在
在![]() 上的下界函数,求实数
上的下界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且以椭圆上的点和长轴两端点为顶点的三角形的面积的最大值为
,且以椭圆上的点和长轴两端点为顶点的三角形的面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)经过定点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() 、
、![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,试证明:直线
,试证明:直线![]() 与
与![]() 轴的交点
轴的交点![]() 为一个定点,且
为一个定点,且![]() (
(![]() 为原点).
为原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,满足
,满足![]() ,则( )
,则( )
A.函数![]() 有2个极小值点和1个极大值点
有2个极小值点和1个极大值点
B.函数![]() 有2个极大值点和1个极小值点
有2个极大值点和1个极小值点
C.函数![]() 有可能只有一个零点
有可能只有一个零点
D.有且只有一个实数![]() ,使得函数
,使得函数![]() 有两个零点
有两个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为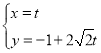 (
(![]() 为参数). 以
为参数). 以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)若![]() ,求
,求![]() ;
;
(2)若点![]() 是曲线
是曲线![]() 上不同于
上不同于![]() 的动点,求
的动点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com