

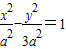 ,从而可得∠BOx=60°,可求得B(2,2
,从而可得∠BOx=60°,可求得B(2,2 ),A(2,
),A(2,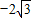 ),根据点P分线段AB所成的比为3:1得P(2,
),根据点P分线段AB所成的比为3:1得P(2,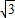 ),代入双曲线方程,即可求出双曲线M的方程;
),代入双曲线方程,即可求出双曲线M的方程;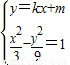 ,消去y得(k2-3)x2+2kmx+m2+9=0
,消去y得(k2-3)x2+2kmx+m2+9=0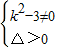 ,从而有
,从而有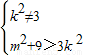
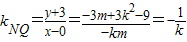
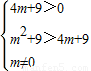 ,从而求出实数m的取值范围.
,从而求出实数m的取值范围.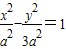
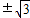
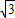 ),A(2,
),A(2,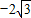 )
)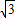 ),代入双曲线方程得a2=3,
),代入双曲线方程得a2=3,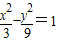
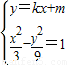 ⇒(k2-3)x2+2kmx+m2+9=0
⇒(k2-3)x2+2kmx+m2+9=0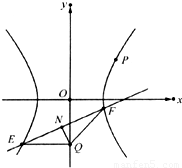 设E(x1,y1)、F(x2,y2),线段EF的中点为N(x,y),则有
设E(x1,y1)、F(x2,y2),线段EF的中点为N(x,y),则有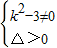 ⇒
⇒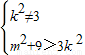 ①
①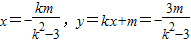

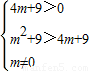
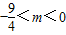


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
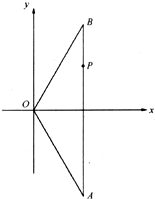 (2006•广州一模)如下图,在△OAB中,|OA|=|OB|=4,点P分线段AB所成的比为3:1,以OA、OB所在直线为渐近线的双曲线M恰好经过点P,且离心率为2.
(2006•广州一模)如下图,在△OAB中,|OA|=|OB|=4,点P分线段AB所成的比为3:1,以OA、OB所在直线为渐近线的双曲线M恰好经过点P,且离心率为2.查看答案和解析>>
科目:高中数学 来源:导学大课堂选修数学2-1苏教版 苏教版 题型:044
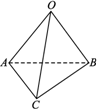
如下图,在空间四边形OABC中,OA=8,AB=6,AC=4,BC=5,∠OAC=45°,∠OAB=60°,求OA与BC夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2006年广东省广州市高考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2009年江苏省南通市启东中学高考数学模拟试卷8(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com