
【题目】已知当![]() ,函数
,函数![]() ,且
,且![]() ,若
,若![]() 的图像与
的图像与![]() 的图像在第二象限有公共点,且在该点处的切线相同,当实数
的图像在第二象限有公共点,且在该点处的切线相同,当实数![]() 变化时,实数
变化时,实数![]() 的取值范围是_______.
的取值范围是_______.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在宽为![]() 的路边安装路灯,灯柱
的路边安装路灯,灯柱![]() 高为
高为![]() ,灯杆
,灯杆![]() 是半径为
是半径为![]() 的圆
的圆![]() 的一段劣弧.路灯采用锥形灯罩,灯罩顶
的一段劣弧.路灯采用锥形灯罩,灯罩顶![]() 到路面的距离为
到路面的距离为![]() ,到灯柱所在直线的距离为
,到灯柱所在直线的距离为![]() .设
.设![]() 为灯罩轴线与路面的交点,圆心
为灯罩轴线与路面的交点,圆心![]() 在线段
在线段![]() 上.
上.

(1)当![]() 为何值时,点
为何值时,点![]() 恰好在路面中线上?
恰好在路面中线上?
(2)记圆心![]() 在路面上的射影为
在路面上的射影为![]() ,且
,且![]() 在线段
在线段![]() 上,求
上,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用![]() 表示活动推出的天数,
表示活动推出的天数,![]() 表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:
表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:
表1:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 6 | 11 | 21 | 34 | 66 | 101 | 196 |
根据以上数据,绘制了散点图.
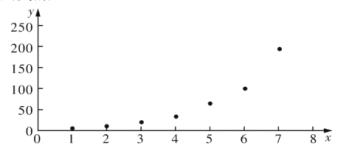
(1)根据散点图判断,在推广期内,![]() 与
与![]() (
(![]() 均为大于零的常数)哪一个适宜作为扫码支付的人次
均为大于零的常数)哪一个适宜作为扫码支付的人次![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型?(给出判断即可,不必说明理由).
的回归方程类型?(给出判断即可,不必说明理由).
(2)根据(1)的判断结果及表1中的数据,建立![]() 关于
关于![]() 的回归方程,并预测活动推出第8天使用扫码支付的人次.
的回归方程,并预测活动推出第8天使用扫码支付的人次.
(3)推广期结束后,为更好的服务乘客,车队随机调查了100人次的乘车支付方式,得到如下结果:
表2
支付方式 | 现金 | 乘车卡 | 扫码 |
人次 | 10 | 60 | 30 |
已知该线路公交车票价2元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受8折优惠,扫码支付的乘客随机优惠,根据调査结果发现:使用扫码支付的乘客中有5名乘客享受7折优惠,有10名乘客享受8折优惠,有15名乘客享受9折优惠.预计该车队每辆车每个月有1万人次乘车,根据所给数据,以事件发生的频率作为相应事件发生的概率,在不考虑其他因素的条件下,按照上述收费标准,试估计该车队一辆车一年的总收入.
参考数据:
|
|
|
|
|
62.14 | 1.54 | 2535 | 50.12 | 3.47 |
其中![]() .
.
参考公式:
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: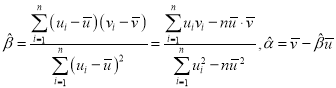 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2013年5月,华人数学家张益唐的论文《素数间的有界距离》在《数学年刊》上发表,破解了困扰数学界长达一个多世纪的难题,证明了孪生素数猜想的弱化形式,即发现存在无穷多差小于7000万的素数对.这是第一次有人证明存在无穷多组间距小于定值的素数对.孪生素数猜想是希尔伯特在1900年提出的23个问题中的第8个,可以这样描述:存在无穷多个素数![]() ,使得
,使得![]() 是素数,素数对
是素数,素数对![]() 称为孪生素数.在不超过16的素数中任意取出不同的两个,则可组成孪生素数的概率为( )
称为孪生素数.在不超过16的素数中任意取出不同的两个,则可组成孪生素数的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左顶点为
的左顶点为![]() ,过点
,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 轴上方一点
轴上方一点![]() ,以
,以![]() 为边作矩形
为边作矩形![]() ,其中直线
,其中直线![]() 过原点
过原点![]() .当点
.当点![]() 为椭圆
为椭圆![]() 的上顶点时,
的上顶点时,![]() 的面积为
的面积为![]() ,且
,且![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)求矩形![]() 面积
面积![]() 的最大值;
的最大值;
(3)矩形![]() 能否为正方形?请说明理由.
能否为正方形?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为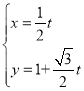 (t为参数),以直角坐标系
(t为参数),以直角坐标系![]() 的
的![]() 点为极点,
点为极点,![]() 为极轴,且长度单位相同,建立极坐标系,得曲线
为极轴,且长度单位相同,建立极坐标系,得曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的倾斜角;
的倾斜角;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁超市旗舰店在元旦当天推出一个购物满百元抽奖活动,凡是一次性购物满百元者可以从抽奖箱中一次性任意摸出2个小球(抽奖箱内共有5个小球,每个小球大小形状完全相同,这5个小球上分别标有1,2,3,4,5 这5个数字).
(1)列出摸出的2个小球的所有可能的结果.
(2)已知该超市活动规定:摸出的2个小球都是偶数为一等奖;摸出的2个小球都是奇数为二等奖.请分别求获得一等奖的概率与获得二等奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设三棱锥![]() 的底面是正三角形,侧棱长均相等,
的底面是正三角形,侧棱长均相等,![]() 是棱
是棱![]() 上的点(不含端点),记直线
上的点(不含端点),记直线![]() 与直线
与直线![]() 所成角为
所成角为![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,二面角
,二面角![]() 的平面角为
的平面角为![]() ,则( )
,则( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com