
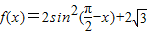 sin(π-x)cosx,
sin(π-x)cosx,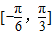 上的值域;
上的值域;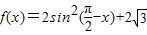 sin(π-x)cosx转化为:
sin(π-x)cosx转化为: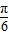 ),由x∈
),由x∈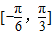 ⇒2x+
⇒2x+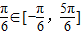 ,由正弦函数的图象与性质可求得函数f(x)在
,由正弦函数的图象与性质可求得函数f(x)在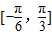 上的值域;
上的值域;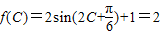 ,0<C<π⇒C=
,0<C<π⇒C=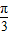 ;2sinB=cos(A-C)-cos(A+C)⇒sinB=sinAsinC
;2sinB=cos(A-C)-cos(A+C)⇒sinB=sinAsinC ,
,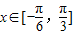 时,2x+
时,2x+ ,
,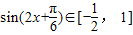 ,2sin(2x)+1∈[0,3],即f(x)∈[0,3];
,2sin(2x)+1∈[0,3],即f(x)∈[0,3];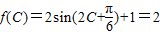 ,
,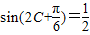 ,0<C<π,所以C=
,0<C<π,所以C=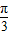 ,
,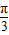 ,A+B+C=π可得:
,A+B+C=π可得: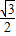 sinA,即sinAcosC+cosAsinC=
sinA,即sinAcosC+cosAsinC=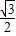 sinA,
sinA,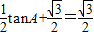 tanA,
tanA,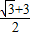 .
.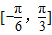 ⇒2x+
⇒2x+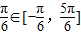 ,再利用正弦函数的图象与性质予以解决,(2)着重考查三角函数的恒等变换及化简求值,属于中档题.
,再利用正弦函数的图象与性质予以解决,(2)着重考查三角函数的恒等变换及化简求值,属于中档题. 

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
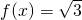 sin(ωx-
sin(ωx- )-cos(ωx-
)-cos(ωx- )(ω>0)图象的两相邻对称轴间的距离为
)(ω>0)图象的两相邻对称轴间的距离为 .
. )的值;
)的值; 个单位后,得到函数y=g(x)图象,求g(x)在区间[0,
个单位后,得到函数y=g(x)图象,求g(x)在区间[0, ]上的单调性.
]上的单调性.查看答案和解析>>
科目:高中数学 来源:2008-2009学年重庆八中高三(下)第二次月考数学试卷(理科)(解析版) 题型:解答题
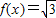 sin(ωx-
sin(ωx- )-cos(ωx-
)-cos(ωx- )(ω>0)图象的两相邻对称轴间的距离为
)(ω>0)图象的两相邻对称轴间的距离为 .
. )的值;
)的值; 个单位后,得到函数y=g(x)图象,求g(x)在区间[0,
个单位后,得到函数y=g(x)图象,求g(x)在区间[0, ]上的单调性.
]上的单调性.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
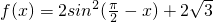 sin(π-x)cosx,
sin(π-x)cosx, 上的值域;
上的值域;查看答案和解析>>
科目:高中数学 来源:重庆市月考题 题型:解答题
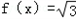 sin(
sin(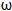 x﹣
x﹣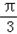 )﹣cos(
)﹣cos(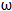 x﹣
x﹣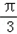 )(
)(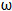 >0)图象的两相邻对称轴间的距离为
>0)图象的两相邻对称轴间的距离为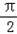 .
. 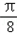 )的值;
)的值;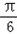 个单位后,得到函数y=g(x)图象,求g(x)在区间[0,
个单位后,得到函数y=g(x)图象,求g(x)在区间[0,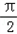 ]上的单调性.
]上的单调性.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com