
【题目】已知函数f(x)=aln(x+1)﹣x2 , 在(1,2)内任取两个实数x1 , x2(x1≠x2),若不等式 ![]() >1恒成立,则实数a的取值范围为( )
>1恒成立,则实数a的取值范围为( )
A.(28,+∞)
B.[15,+∞)
C.[28,+∞)
D.(15,+∞)
科目:高中数学 来源: 题型:
【题目】某研究所设计了一款智能机器人,为了检验设计方案中机器人动作完成情况,现委托某工厂生产![]() 个机器人模型,并对生产的机器人进行编号:
个机器人模型,并对生产的机器人进行编号: ![]() ,采用系统抽样的方法抽取一个容量为
,采用系统抽样的方法抽取一个容量为![]() 的机器人样本,试验小组对
的机器人样本,试验小组对![]() 个机器人样本的动作个数进行分组,频率分布直方图及频率分布表中的部分数据如图所示,请据此回答如下问题:
个机器人样本的动作个数进行分组,频率分布直方图及频率分布表中的部分数据如图所示,请据此回答如下问题:
分组 | 机器人数 | 频率 |
| 0.08 | |
| 10 | |
| 10 | |
| ||
| 6 |

(1)补全频率分布表,画出频率分布直方图;
(2)若随机抽的第一个号码为![]() ,这
,这![]() 个机器人分别放在
个机器人分别放在![]() 三个房间,从
三个房间,从![]() 到
到![]() 在
在![]() 房间,从
房间,从![]() 到
到![]() 在
在![]() 房间,从
房间,从![]() 到
到![]() 在
在![]() 房间,求
房间,求![]() 房间被抽中的人数是多少?
房间被抽中的人数是多少?
(3)从动作个数不低于![]() 的机器人中随机选取
的机器人中随机选取![]() 个机器人,该
个机器人,该![]() 个机器人中动作个数不低于
个机器人中动作个数不低于![]() 的机器人记为
的机器人记为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣a(1﹣ ![]() ).
).
(1)若a=1,求f(x)的单调区间;
(2)若f(x)≥0,对任意的x≥1均成立,求实数a的取值范围;
(3)求证:( ![]() )1008>
)1008> ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣lnx﹣1,若曲线y=f(x)在点(2,f(2))处的切线与直线2x+y﹣1=0垂直.
(1)求a的值;
(2)函数g(x)=f(x)﹣m(x﹣1)(m∈R)恰有两个零点x1 , x2(x1<x2),求函数g(x)的单调区间及实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取![]() 名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试,测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子停下所需要的距离),无酒状态与酒后状态下的试验数据分别列于表
名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试,测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子停下所需要的距离),无酒状态与酒后状态下的试验数据分别列于表![]()
停车距离 |
|
|
|
|
|
频数 | 26 |
|
| 8 | 2 |
表![]()
平均每毫升血液酒精含量 | 10 | 30 | 50 | 70 | 90 | /tr>
平均停车距离 | 30 | 50 | 60 | 70 | 90 |
已知表![]() 数据的中位数估计值为
数据的中位数估计值为![]() ,回答以下问题.
,回答以下问题.
(Ⅰ)求![]() 的值,并估计驾驶员无酒状态下停车距离的平均数;
的值,并估计驾驶员无酒状态下停车距离的平均数;
(Ⅱ)根据最小二乘法,由表![]() 的数据计算
的数据计算![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(Ⅲ)该测试团队认为:驾驶员酒后驾车的平均“停车距离”![]() 大于(Ⅰ)中无酒状态下的停车距离平均数的
大于(Ⅰ)中无酒状态下的停车距离平均数的![]() 倍,则认定驾驶员是“醉驾”.请根据(Ⅱ)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
倍,则认定驾驶员是“醉驾”.请根据(Ⅱ)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
(附:回归方程![]() 中,
中, 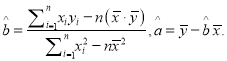 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行抽奖活动,规则如下:甲箱子里装有3个白球和2个黑球,乙箱子里装有1个白球和3个黑球,这些球除颜色外完全相同;每次抽奖都从这两个箱子里各随机地摸出2个球,若摸出的白球个数不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)在一次游戏中,求获奖的概率;
(2)在三次游戏中,记获奖次数为随机变量X,求X的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知映射f:A→B,其中A=B=R,对应法则f:x→y=( ![]() )
) ![]() ,若对实数m∈B,在集合A中存在元素与之对应,则m的取值范围是( )
,若对实数m∈B,在集合A中存在元素与之对应,则m的取值范围是( )
A.(﹣∞,2]
B.[2,+∞)
C.(2,+∞)
D.(0,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的上下两个焦点分别为
的上下两个焦点分别为![]() ,过点
,过点![]() 与
与![]() 轴垂直的直线交椭圆
轴垂直的直线交椭圆![]() 于
于![]() 两点,
两点, ![]() 的面积为
的面积为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() 为坐标原点,直线
为坐标原点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() 两个不同的点,若
两个不同的点,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com