
【题目】已知椭圆![]() :
: ![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,过点
,过点![]() 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,
, ![]() .
.
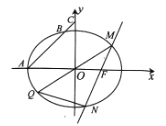
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,连接
两点,连接![]() (
(![]() 为坐标原点)并延长交椭圆
为坐标原点)并延长交椭圆![]() 于点
于点![]() ,求
,求![]() 面积的最大值及取最大值时直线
面积的最大值及取最大值时直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】在公比为正数的等比数列{an}中, ![]() ,
, ![]() ,数列{bn}(bn>0)的前n项和为Sn满足
,数列{bn}(bn>0)的前n项和为Sn满足 ![]() (n≥2),且S10=100.
(n≥2),且S10=100.
( I)求数列{an}和数列{bn}的通项公式;
( II)求数列{anbn}的前n项和为Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 上的点到二定点
上的点到二定点![]() 、
、![]()
![]() 的距离之和为定值
的距离之和为定值![]() ,以
,以![]() 为圆心半径为4的圆
为圆心半径为4的圆![]() 与
与![]() 有两交点,其中一交点为
有两交点,其中一交点为![]() ,
, ![]() 在y轴正半轴上,圆
在y轴正半轴上,圆![]() 与x轴从左至右交于
与x轴从左至右交于![]() 二点,
二点, ![]() .
.
(1)求曲线![]() 、
、![]() 的方程;
的方程;
(2)曲线![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() ,过
,过![]() 点的直线
点的直线![]() 与曲线
与曲线![]() 交于
交于![]() 二点,过
二点,过![]() 做
做![]() 的切线
的切线![]() ,
, ![]() 交于
交于![]() .当
.当![]() 在x轴上方时,是否存在点
在x轴上方时,是否存在点![]() ,满足
,满足![]() ,并说明理由.
,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某印刷厂的打印机每5年需淘汰一批旧打印机并购买新机,买新机时,同时购买墨盒,每台新机随机购买第一盒墨150元,优惠0元;再每多买一盒墨都要在原优惠基础上多优惠一元,即第一盒墨没有优惠,第二盒墨优惠一元,第三盒墨优惠2元,……,依此类推,每台新机最多可随新机购买25盒墨.平时购买墨盒按零售每盒200元.
公司根据以往的记录,十台打印机正常工作五年消耗墨盒数如下表:
消耗墨盒数 | 22 | 23 | 24 | 25 |
打印机台数 | 1 | 4 | 4 | 1 |
以这十台打印机消耗墨盒数的频率代替一台打印机消耗墨盒数发生的概率,记ξ表示两台打印机5年消耗的墨盒数.
(1)求ξ的分布列;
(2)若在购买两台新机时,每台机随机购买23盒墨,求这两台打印机正常使用五年在消耗墨盒上所需费用的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子里装有大小均匀的8个小球,其中有红色球4个,编号分别为1,2,3,4;白色球4个,编号分别为2,3,4,5. 从盒子中任取4个小球(假设取到任何一个小球的可能性相同).
(1)求取出的4个小球中,含有编号为4的小球的概率;
(2)在取出的4个小球中,小球编号的最大值设为![]() ,求随机变量
,求随机变量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[﹣1,1]上的奇函数,当x∈[﹣1,0]时,函数的解析式为f(x)= ![]() ﹣
﹣ ![]() (a∈R).
(a∈R).
(1)求出f(x)在[0,1]上的解析式;
(2)求f(x)在[﹣1,0]上的最大值.
(3)对任意的x1 , x2∈[﹣1,1]都有|f(x1)﹣f(x2)|≤M成立,求最小的整数M的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com